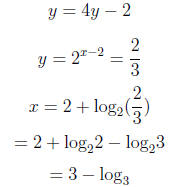1. (B) The original equation is
.
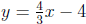The new equation will of the
form
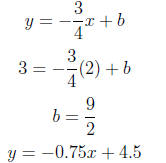
2. (D) The triangle is a right triangle with right angle
at the origin and its
other two vertices as the x-intercept and y-intercept of y = -0.75x+4.5.
In that equation, when y = 0, x = 6. When x = 0,
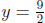. The area of
the triangle is
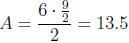
3. (C) The distance from a line Ax + By+ C = 0 to a point
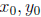is given
by the formula
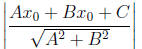
Plugging in values ,
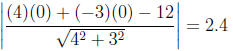
4. (B) Any line which passes through the circle ’s center,
(-3,-2), must
contain a diameter of the circle . If the slope of the equation is m, then
such a line can be described as
y = m(x + 2) - 3
y = mx + 2m - 3
5. (D)
x2 - xc + (c - 1) = 0
Using the quadratic formula ,
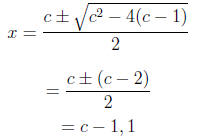
6. (C) In a quadratic Ax2+Bx+C, only one solution exists
if B2-4AC =
0. For this equation,
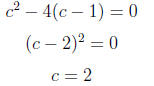
7. (A)
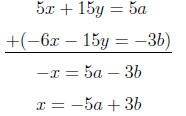
8. (D) For this quadratic, we want the following equation
to be true
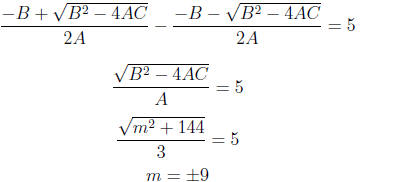
9. (B) Initially, let f(x) = ax2 + bx + c.
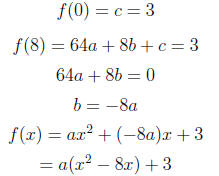
10. (A) Knowing the 2 roots and the constant mulitplier,
we can say that
the form of the quadratic function is f(x) = a(x - 2)(x - 10) This
expands to ax 2 - 12ax + 20a. The x-value of the vertex is
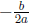, which
is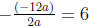 
. f(6) = -16a, making the vertex (6, 16a).
11. (B) Intersections occurs when
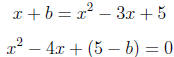
There is only one intersection point when the above
quadratic has only
one solution, i.e. it is a perfect square . This occurs when
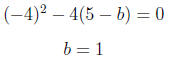
12. (A) Let the quadratic have the form
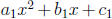and
the cubic have
the form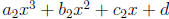 
. The x- values of all intersection points
will satisfy the equation
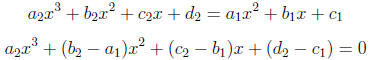
This is a cubic, and the Fundamental Theorem of Algebra
guarantees
that there are no more than 3 solutions for a 3rd degree equation.
However, a cubic and a quadratic must intersect since the cubic has
a steeper graph for larger and smaller values of x. As the values of x
increase (or decrease, depending on the direction of both functions),
the graph of the cubic will “overtake” the graph of the quadratic.
13. (C) The baseball will reach its maximum height when
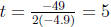
h(5) = 122.5
14. (E) Let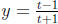 
. If the
y’s and the t’s are switched, then solving for y
arrives at the inverse.
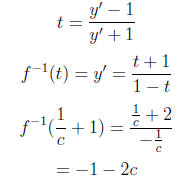
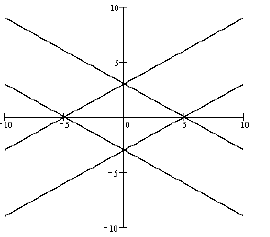
15. (A)
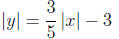
This equation represents four equations which can be
expressed as
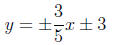
The enclosed area is a rhombus whose diagonals have length
10 and 6,
so the resulting area is
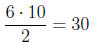
16. (A)
x - y = 100 computers
empty truck = x - 4(100 computers)
= x - 4(x - y)
= 4y - 3x
17. (B)
Let
x = 3 since x > 0
18. (E)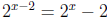 
. Let
.
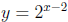