Canceling Terms in Fractions
Once a fraction is in reduced form, you may begin trying
to cancel terms. Only
when factors in the numerator match exactly with factors in the denominator can
the
terms be canceled . One of the most consistent ways to ensure that your
cancellations are
appropriate is to factor the numerator and denominator into smaller pieces
before
attempting to cancel.
Example 1: Simplify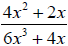 
Solution: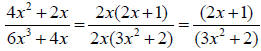
In Example 1, we can factor 2x from both the numerator and
denominator. Thus, we can
cancel the 2x terms from the expression . A common mistake made by students is to
“cancel” pieces that are not factors.
Bad Example 1: Simplify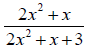 
Bad Solution :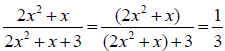 
In this bad example, the term
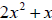is a factor of the numerator, but it
is not a factor of
the denominator. This cancellation is therefore invalid. (verify this by
plugging in a
numerical value for x.)
The Least Common Denominator
You should already be familiar with the standard technique
for adding fractions
together. Generally, we find a common denominator between the terms in our
expression. In order to ensure that the fraction we get as a result of addition
(or
subtraction ) is in reduced form, we are interested in finding the least common
denominator (LCD) for our sum. To find the LCD, write the denominator of each
fraction as a product of its prime factors. The LCD will be the smallest number
that is a
multiple of each denominator .
Example 2: Find the LCD for
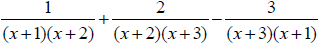
The LCD of this sum is (x + 1)(x + 2)(x + 3).
