Warm-up
1. Does the graph of y =0.02x^2 + 24x – 6 open up or down? up
2. For the system of linear equations x + y = 4 and y = 2x, find the value of x
by
replacing y with 2x in the equation x + y = 4 x = 4/3
3. At what point do the lines x + y = 4 and y = 2x intersect? (4/3, 8/3)
4. If 0.75x = 7.5, what is the value of x ? x = 10
5. In the equation y = 0.04x^2 + 1.7x, find y when x = 2. y = 3.56
Today we will:
1. Solve problems involving quadratic systems.
Tomorrow we will:
1. Review Unit 4
4-7 Quadratic Systems
A quadratic system is two or more quadratic
functions with the same variables.
Solving a quadratic system is the same as finding the
coordinates of the points where two
parabolas intersect .
If the parabolas do not intersect, then there are no
real -number solutions to the system.
You can solve a system graphically or algebraically .
We can solve these using substitution!
Example 1 – Solve the system algebraically.
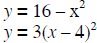
Solution
Substitute 16 – x^2 for y in the second equation.
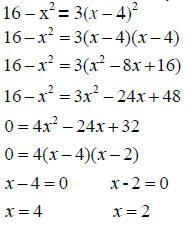
Set the equation equal to 0.–16 and +x^2 to each side
Can use the quadratic formula or factor . The answer will be the same.
Factor: Factor out a 4 and divide both sides by 4
To find y, substitute x -values into one of the equations.
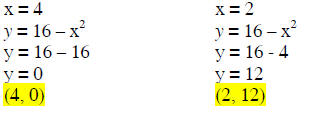
Example 2 - Solve algebraically
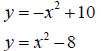
Solution
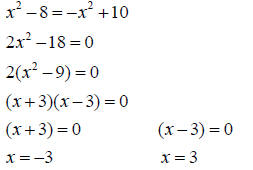
Substitute x -values to find y.
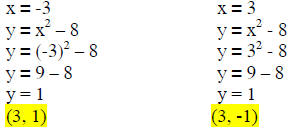
Example 3
Estimate the solutions , then check by substitution.
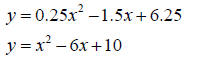
Solution