Algebra deals mainly with equations of one variable.
At the end of MAT 117 (or whatever class you took),
you learned how to solve equations with more than
one variable in them , such as:
x + 3y = -5
4x - 2y = 8
How?
The key to solving these equations is elimination ,
where we multiply (both sides of) one equation by
a number, (both sides of) the other equation by a
number, and add the two new equations:
-4 × (x + 3y = -5)
1 × (4x - 2y = 8)
The key to solving these equations is elimination,
where we multiply (both sides of) one equation by
a number, (both sides of) the other equation by a
number, and add the two new equations:
-4x - 12y = 20
4x - 2y = 8
The key to solving these equations is elimination,
where we multiply (both sides of) one equation by
a number, (both sides of) the other equation by a
number, and add the two new equations:
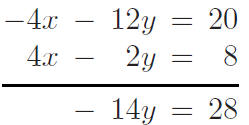
So y = 28/-14 = -2. How do we find x?
We can use elimination to find x , or we can
substitute the value of y into one of the original
equations:
x + 3y = -5
x + 3 • (-2) = -5
x = -5 - 3 • (-2) = 1
This method of finding x is called back substitution.
Going back to the original equations:
x + 3y = -5
4x - 2y = 8
How specifically do we answer the question \What
are the solutions ?"?
Answer: By giving the value of x together with the
value of y, usually as an ordered pair (x, y) = (1,-2)
or as a \vector"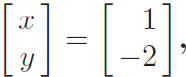 
or as two equations:
x = 1
y = -2
Okay, now what about three equations with three
variables? Such as:
x - y + 2z = 3
2x - 2y + 8z = 22
x - 2y = 2
It's not clear how to come up with an equation with
just one variable in it. However, elimination can
be used to come up with two equations which only
involve the variables y and z. These equations in
turn can be solved for y and z, which in turn will
give us the value of x.
The bad news is that it takes a lot more work and a
lot more care, but it can be done.
But first, it's time for some vocabulary : : :
A linear equation is an equation of the form
number × variable + number
× variable
+ … + number × variable = number
such as:
2x + 3y + 2z = -1
A system of linear equations is one or more linear
equations, which must all be true at the same time.
A system of linear equations is consistent if it has at
least one solution . (Not all systems are consistent!)
A system of linear equations is inconsistent if it has
no solutions.
A system of linear equations is homogeneous if all the
numbers on the right -hand side are 0's. (You may
have run across this term , if you've taken Differential
Equations.)
Two systems of linear equations are equivalent if they
have the same solutions.
