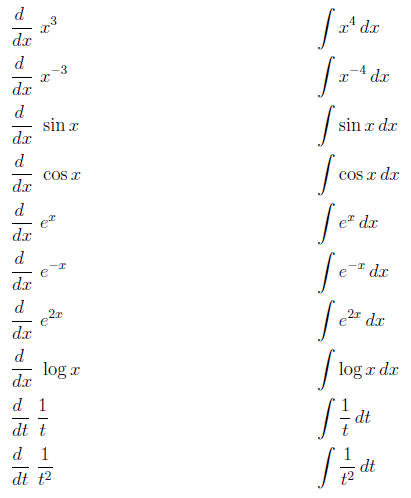A little time spent now reviewing algebra and calculus facts will save you a
lot of time
later. So pull your calculus textbook o the bookshelf and do the following
questions.
(1) Suppose 1/y = x + C. True or false ( circle one ): is
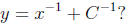
(If you're not sure, then try it with actual values for x and C .)
If false, then find a correct formula for y :
(2) Notation: in mathematics "log" means the same thing as "ln", in other
words the
natural logarithm or logarithm to base e.
Suppose ey = x + 1. True or false (circle one): is y = log x + log 1? If false,
then
find a correct formula for y :
(3) Suppose arcsin y = x + π/6. True or false
( circle one ): is y = sin(x) + sin(π/6)? If
false, then find a correct formula for y:
(4) A quadratic equation ar^2 + br + c = 0 can be solved by factoring
the equation as
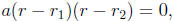
in which case the roots are r = r1 and r = r2, or else by invoking the
quadratic
formula
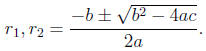
Advice. Since it is often difficult to see how to factor a
quadratic equation , your best
bet is usually to invoke the quadratic formula .
Here are the questions: find the roots of
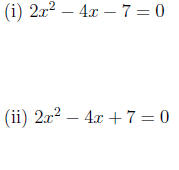
(5) Consider a graph y = f(x). Using that
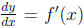equals the slope of the graph at
the point (x, f(x)) on the graph , explain with a picture why it is that
,
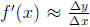where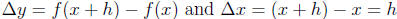 
, and h is small.
[Recall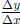 
is called a
difference quotient , and gives the "rise in y" divided by the
"run in x". The difference quotient justifies our interpretation of the
derivative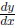 
as
a rate of change of quantity y with respect to changes in quantity x.]
(6) Evaluate the following derivatives, and
antiderivatives (indefinite integrals):
