Division and Factors
Long Division: Do the first half of Example 1.
Divide to determine whether x +1 is a factor of
x 3 + 2x2 −5 x−6
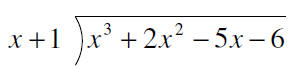
Since the remainder is 0, we know that x +1 is a factor of x 3+ 2x2 − 5x
−6 . In fact, we know
that x3 +2 x2 −5 x −6 =( x + 1)(_____________________)
Synthetic Division :
Example 2: Use synthetic division to find the quotient and remainder: (2x3
+ 7x2 −5) รท (x +3)
The quotient is _________________________, and the remainder is ________.
Section 4.4, Zeros of Polynomial Functions , pp. 332-339,
Summary
Finding Polynomials with Given Zeros
Do Example 1: Find a polynomial function of degree 3, having the zeros 1,
3i, and -3i.
( f x ) = a n ( ____________ )( ____________ )( _____________ )
Since an can be any number, we’ll let it be 1 to get the simplest polynomial.
Multiply these out to understand the next step in the book . Then finish the rest
of the example.
Zeros of Polynomial Functions with Read Coefficients
Nonreal Zeros: a + bi and a + bi , b ≠ 0 : If a complex number a + bi , b ≠0
, is a zero of a
polynomial f (x) with real coefficients , then its conjugate, _______________, is
also a zero.
Irrational Zeros: a +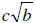 
and a +
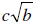, b is not a perfect square:
If a +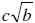 
, where a, b, and c
are rational and b is not a perfect square, is a zero of a polynomial f (x) with
real coefficients, then
its conjugate, _______________, is also a zero.
Example 3: Suppose that a polynomial function of
degree 6 with rational coefficients has − 2 + 5i ,
− 2i , and 1−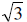 
as three of its zeros. Find
the other zeros.
The other zeros are ______________, ________________, and
_______________.
There are no other zeros because
__________________________________________________
____________________________________________________________________________.
Example 4: Find a polynomial function of lowest
degree with rational coefficients that has
1− 2 and 1+ 2i as two of its zeros.
Section 4.5, Rational Functions , pp. 342-356, Summary
A rational function is a function f that is a quotient of two polynomials.
That is,
f (x) =_________ , where p(x) and q(x) are polynomials and where q(x) is not the zero
polynomial. The domain of f consists of all inputs x for which
_________________.
Determining Vertical Asymptotes: For a rational
function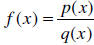 
where p(x) and q(x) are
polynomials with no common factors other than constants, if a is a ____________
____ ____
__________________, then the line ________ = _________ is a vertical asymptote
for the graph of
the function .
Determining a Horizontal Asymptote:
• When the numerator and denominator of a rational function have the same
degree, the line
_____ = _____ is the horizontal asymptote, where a and b are the leading
coefficients of
the numerator and the denominator, respectively.
• When the degree of the numerator of a rational function is less than the
degree of the
denominator , the ___-axis, or _____ = ______ , is the horizontal asymptote.
• When the degree of the numerator of a rational function is greater than the
degree of the
denominator, there is ______ _________________ ___________________.
Oblique Asymptote: An oblique asymptote occurs when
the degree of the numerator is ____
___________ _______ the degree of the denominator (see page 351).
Example 7: Find all asymptotes of
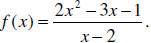
Vertical asymptote:
because _________________________________.
Horizontal asymptote:
because _________________________________.
Oblique asymptote: Divide 2x2 −3 x −1 by x − 2 .
Thus, the line y = _______________ is the oblique
asymptote.
