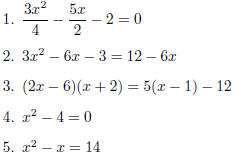In groups of about 4, complete each of the following 5
parts. You need not do them in order, but you should
do part 5 last. (If you are less familiar with foiling and factoring, I suggest
starting with step 1 and going
through in order . You should have one piece of paper per group with solutions to
the questions for each
part.
Part I
Algebra Blocks
Send up one representative to get the algebra blocks and get a quick demo of how
they are used.
Multiply the following binomials together using the algebra blocks. (Use the
L-shaped piece. Choose one of
the unknow lengths for x and line up the parts of each binomial, one per side.
Now ll in the center with
pieces that match each side.)
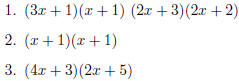
Now, use the blocks the other way, factor the following
quadratics. Grab enough pieces to have the equations
and arrange them in a rectangle. Choose two adjacent sides and see what the
factors are.
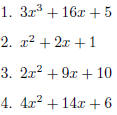
Part II
Factoring by grouping
One method of factoring quadratics (without guess and check) relies on factoring
by grouping. Here is an
example of factoring by grouping.
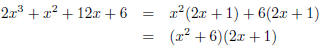
The method goes like this . Make sure your quadratic is
written in the form ax2 + bx + c. Note what a, b,
and c are equal to. Now find the product ac. Find two factors of the number ac
that add up to b. Rewrite
your b term as the sum of those factors. Finally factor by grouping.
Here is an example.
| 5x2 + 11x + 2 |
So a = 5, b = 11, and c = 2 |
| ac = 5· 2= 10 |
So my product of ac is 10 |
| 10 ·1 = 10 and 10 + 1 = 11 |
So I choose 10 and 1 to be my factors of ac that
add up to b |
| 5x2 + 11x + 2
= 5x2 + 10x + 1x + 2 |
| |
Now that I have rewritten 11x as 10x + 1x I
factor by grouping |
| 5x(x + 2) + 1(x + 2) = (5x + 1)(x +
2) |
Thus I can factor 5x2 + 11x + 2 as (5x + 1)(x + 2). Now you try some.
1. 4x2 + 7x - 15 (Hint: Since c is negative, one of the factors of ac
will be positive, the other will be
negative )
2. x2 + 5x + 4
3. x2 + 8x + 15
4. x2 - 7x + 12 (Hint: Since b is negative and c is positive, both
factors of ac will be negative)
Part III
The Zero-Product Property
Let A and B be some unknow expressions. If A ·B = 0 what do I know about A and
B? Well, if the product
is 0, then either A had to be zero or B had to be 0. This is known as the
Zero-Product Property. If we
have to solve a quadratic equation (that can be factored), we will use this
property to find our solutions.
For example:

Do you see how I used the Zero-Product Property on the 3rd
line? Now you try solve some equations using
the Zero-Product Property.
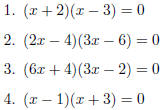
Part IV
The Quadratic Formula
If I have a quadratic written in the form ax2 +bx+c = 0, then I can
use the quadratic formula to find what
x is. The quadratic formula is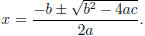 An example:
Solve 2x2 + 3x - 1 = 0. So here I have
An example:
Solve 2x2 + 3x - 1 = 0. So here I have
a = 2, b = 3, c = -1. Now I substitute these into my
formula as follows:
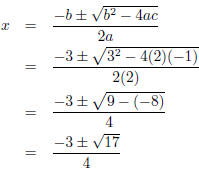
I cannot simplify my expression any more, so my solutions
are 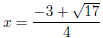 and
and 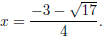
There is a song that can be used to memorize that can be used to memorize the
quadratic formula. It is to
the tune of "Pop goes the weasel" and can be found if you rummage around my
website. Find it and come
show me where it can be found to get credit for doing so. Now you try some:
1. 2x2 + 9x - 5 = 0
2. 2x2 = 4x + 1 (Hint: Be sure to write this in the form ax2
+ bx + c = 0 before applying the formula.)
3. 9x2 - 12x - 5 = 0
4. x2- x = 14 (Hint: See hint on 1 in this section.)
Part V
Wrapping it all up
It's go time! Solve the following equations using the method of your choice.