Conic Sections Lab

Goals

By the end of this lab you should:
1.) Be familar with the important features of hyperbolas, namely their vertices and
asymptotes.
2.) Understand the connection between the equation of the hyperbola and its vertices
and asymptotes.
3.) Be able to draw hyperbolas whose equations are in standard form.
4.) Be able to draw contour diagrams of some important quadratic functions

Introduction

Calculus is about functions. Some basic examples are linear functions like f(x, y) =
3x + 4y and quadratic functions like g (x, y) = 3x² + 4y² or h(x, y, z) = 3x² + 4y² − z².
Calculus is powerful, because it often reduces understanding a complicated function to
understanding a linear or quadratic one. Still, we have to understand the linear and
quadratic functions. In order to understand a quadratic function like g(x, y) = 3x² − 4y²,
we have to understand its levels. These are the curves g (x, y) = c, and they are examples
of hyperbolas.

In this computer lab, we will review hyperbolas. We will need to be able to draw these
curves so that we can draw level curves of quadratic functions. It will turn out that the
pattern of level curves around the critical points of a function of two variables in “most”
cases looks like a family of concentric ellipses or hyperbolas .

Specifically, in this lab you will examine the equations of hyperbolas in standard form,
see how the shape of the hyperbola is related to the terms of the equation, and review how
to draw the graphs of the equations .

This lab will also introduce you to the MAPLE software package, which is an extremely
powerful tool for doing mathematical calculations and graphing.

Background

As we all know, the equation x² + y² − 1 = 0 describes a circle in the xy-plane. In
general, quadratic equations of the form

Ax² + Bxy + Cy² + Dx + Ey + F = 0

describe plane curves known as conic sections . For different choices of the constants
A,B,C,D,E, F you can get an ellipse, hyperbola, parabola, pair of lines, a single line or
a point as the graph of the equation. These sets are called conic sections because they are
the sets you can get if you intersect a cone with a plane.

Hyperbolas

The graph of the equation x²/a²−y²/b² = 1 is a hyperbola in standard form. The
x and y axes are lines of symmetry for this shape. (We say a line L is a line of symmetry
for a shape if L divides the shape into 2 congruent pieces, and the two pieces match if we
rotate one around L.) The hyperbola has two points which are closest to the origin; these
are called vertices, and they lie on the x-axis, if the hyperbola is in standard form.

The hyperbola also has two asymptotes. The equations for the asymptotes are gotten
by taking the quadratic function x²/a² − y²/b², setting it equal to zero, factoring it, and
setting each factor equal to zero. The two equations for the asymptotes that we get are:

x/a + y/b = 0

and

x/a − y/b = 0

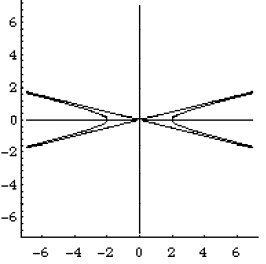
The figure below is a hyperbola, with vertices at (-2,0), (2,0) and with asymptotes 4y = x,
−4y = x. So that you can see how closely the hyperbola hugs the asymptotes, we have
included them in the figure.

Question 1.

(a) Plot x²/a²−y² = 1 for a = 1, 3, 5, 7. We suggest you use a do loop of the following
form. (The MAPLE code is explained in the glossary just before the lab)




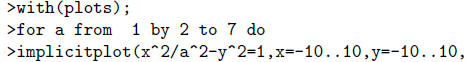
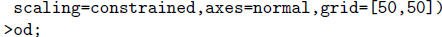
You may also use the following commands.



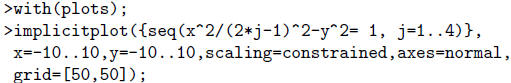
These commands run faster, but they put all the plots in the same window, so you
should be sure you know which values of a go with which plots. Remember that a = 2 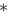j−1.
Don’t print the plots unless you need to refer to them!

(b) Describe the changes you see in the graph as the coefficient a increases . (Make
sure you mention how the asymptotes and vertices change. If you forget what
the asymptotes are or how to find their equations, look back in the introduction
to this lab in the material on hyperbolas.)

(c) Plot x² − y²/b² = 1 for b = 1, 3, 5, 7.
Describe the changes you see in the graph as the coefficient b increases. (Make
sure you mention how the asymptotes and vertices change.)

Question 2. Find the equation of a hyperbola whose asymptotes have slope 1 and −1,
and whose vertices are located at (−6, 0), (6, 0).

Attach a printout of the graph of your hyperbola.

Question 3. Plot x² − y² = c for c = −4,−2, 0, 2, 4.
Describe the changes you see in the graph as the coefficient c increases.

Question 4. Use the commands



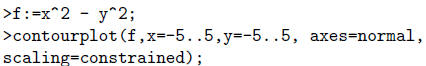
to plot the level curves of f. Based on what you learned from the last question, label those
contours where the value of f is closest to -16,-4,0,4,16. Attach your plot to this lab. Your
MAPLE plot may have left out part of a level curve; if so, fill in the missing part and circle
it. Notice that the asymptotes are level 0 of the function, and all the hyperbolas have the
same asymptotes.

Drawing Hyperbolas by Hand

To draw a hyperbola, first plot the vertices, then draw the asymptotes, then draw
the hyperbola so that it passes through the vertices, and approaches the asymptotes as it
moves away from the vertices.

Question 5. To test what you have learned in the lab, draw the following hyperbolas by
hand.

Question 6. Now draw the contour diagrams of the following functions. Make sure your
diagram includes level 1.

Question 7. Write a paragraph describing the steps you followed in drawing the diagram
in 6a). (Try to include all relevant details. The better you understand what you are doing,
the easier it will be to describe it.)