Primes!
•Definition: A prime is a positive whole number that cannot
be divided evenly by anything except 1 and itself.
Examples
• Awesome Property : Every rational number can be written
as a product of primes to a power .
Examples
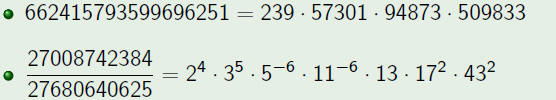
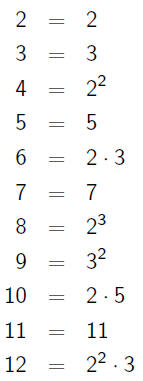
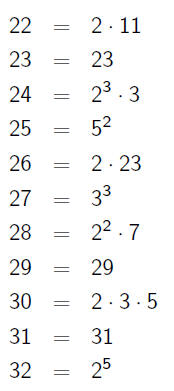
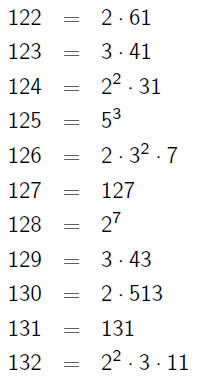
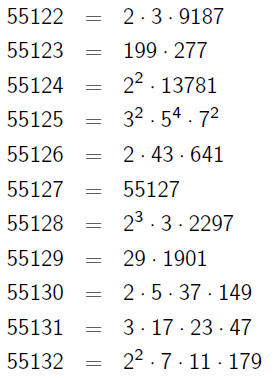
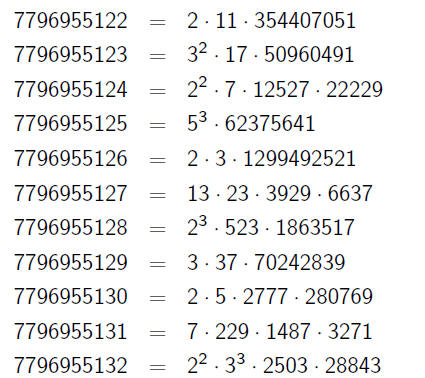
Things We Notice
•a and a + 1 have wildly different factorizations
•As a gets really big, the factorizations become mostly "large"
primes ( like 2503) to a small power (like 1). (Demo)
•Some rare gems are still "small" primes to a "large" power,
e.g.
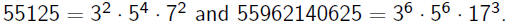
•We call these numbers smooth.
Relationships of Prime Factorizations
•If I know the prime factorization of a and b, then it's easy to
find the prime factorization of ab.
Example
•But what about a + b?
Example
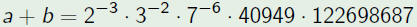
ABC Triples
•(smooth)*(smooth) = smooth
•(smooth)+(smooth) = probably not smooth
BUT SOMETIMES IT IS!
Examples
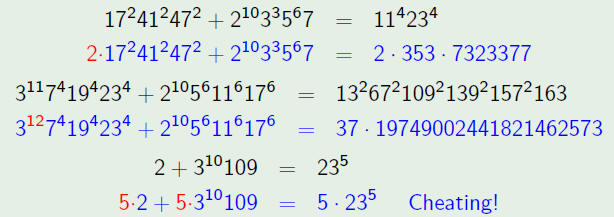
Judging ABC triples
Examples
Better Example: (0.96132)
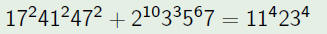
Okay Example: (0.90013)
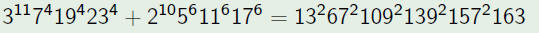
Best Example: (1.62991)
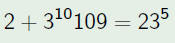
Typical Example: (0.36287)
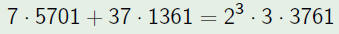
Measuring ABC triples
Definition
The radical of a number , rad(n), is the product of all the primes
dividing n.
Example:
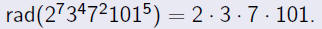
Definition
The ABC Ratio of a triple A + B = C is given by
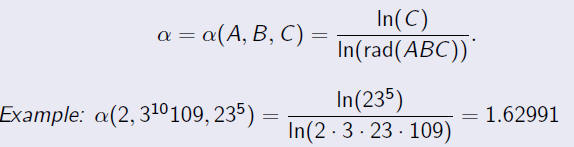
Good ABC Triples
•Top three known ABC ratio (verified up to 1020):
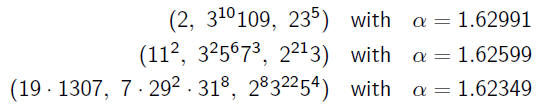
Definition
A good ABC triple is A + B = C where α(A, B, C) >
1.4.
•Largest known good ABC triples:
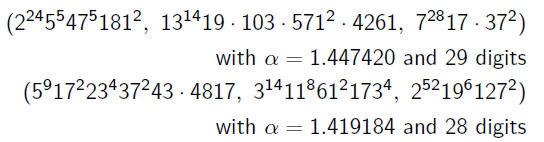
ABC Conjecture
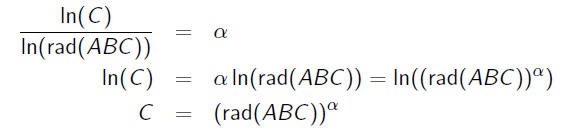
ABC Conjecture (Oesterle and Masser, 1985)
For every η > 1, there exists only a finite number of
ABC triples
such that
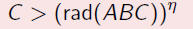
i.e. with
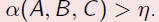
Consequences
Corollary
There is a largest α(A, B, C). It might be 1:62991.
Corollary
If the largest α < 2, then Fermat's Last Theorem
(no integer
solutions to
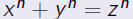for n > 2) is proved.
Proof: Suppose there was a solution, then let A = xn, B = yn,
C = zn.
Then rad(ABC)≤xyz≤z3. Applying the conjecture gives
zn < (rad(ABC))2≤(z3)2 = z6. Hence n≤6.
The cases of 3≤n≤6 were proved in 1825 by Legendre and
Dirichlet.
More Consequences
Corollary
If the ABC conjecture is true then the following are also
proved:
|
•The generalized Fermat |
•Mordell's conjecture |
| equation |
•Roth's theorem |
|
•Wieferich primes statement |
•Dressler's conjecture |
|
•The Erdos-Woods |
•Bounds for the order of the |
| conjecture |
Tate- Shafarevich group |
|
•Hall's conjecture |
•Vojta's height conjecture |
|
•The Erdos-Mollin-Walsh |
•Greenberg's conjecture |
| conjecture |
•The Schinzel-Tijdeman |
|
•Brocard's Problem |
conjecture |
|
•Szpiro's conjecture |
•Lang's conjecture |
... and many more!
How Close Are We to a Proof?
ABC Conjecture (Rephrased)
Given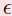 
> 0, there
exists a constant 
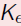such that for every A, B,
C
coprime integers with A + B = C,
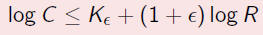
where R = rad(ABC).
Theorem (Gyory (2007))
Let A, B, C be coprime integers with A + B = C. Let t be
the
number of prime factors in R = rad(ABC). Then
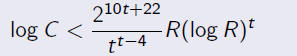
An Analogy
Often a strong analogy between integers and polynomials
with
rational coefficients .
A prime polynomial is one that cannot be factorized into
smaller polynomials with rational coefficents .
Example: x^2 + 1 is prime, but x^2 - 1 = (x + 1)(x - 1) is not.
(But x + 1 and x - 1 are.)
Let rad(P) be the product of all prime polynomials dividing P.
Example: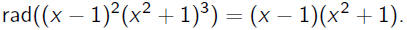 
Let deg(P) be the degree of the polynomial. Notice that
deg(PQ) = deg(P) + deg(Q)
which is just like ln (AB) = ln(A) + ln(B).
The PQR Theorem
Replace A, B, C with polynomials P, Q, and R and replace
ln
with deg.
PQR Theorem (Hurwitz, Stothers, Mason)
Let P, Q, R be nonconstant relatively-prime polynomials
that
satisfy P + Q = R, then
deg(R) < deg(rad(PQR)):
PQR Proof
•First notice that
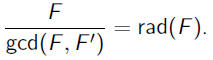
•Example:
| F |
= |
 |
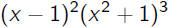| then F' |
= |
 |
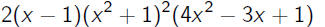| so gcd(F, F') |
= |
 |
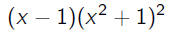and
 |
= |
 |
•
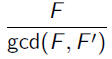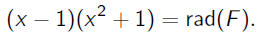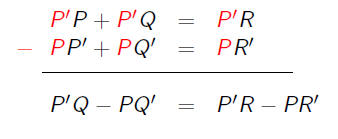
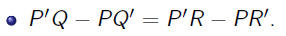
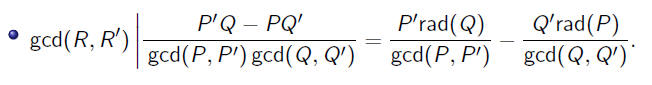
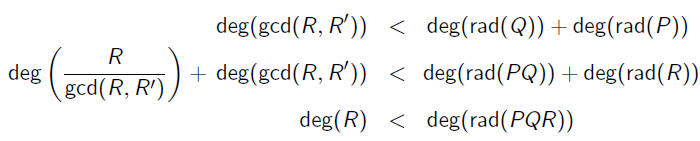
What I Did
The ABC Conjecture can be generalized to number fields
Q(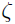
) where 
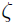is the root of a rational polynomial.
Example (Dokchitser)
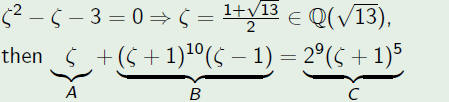
•This triple has algebraic ABC Ratio of 2.029.
There are "interesting" surfaces in algebraic geometry
with
"special" points that correspond to algebraic numbers .
•The corresponding algebraic numbers satisfy
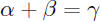and
are usually smooth.
•I used some algorithms developed in my thesis to generate 350
of these examples and computed their algebraic ABC ratios.
Results
•Points given in order of the degree of the defining
polynomial.
•None of these "special" points correspond to a good ABC
example.
•Data does follow a trend. Proof? No idea how to even begin.
•Failure? Well, yes, but no.
The End?
Thanks!
