Section 4-1: Learning Objectives
In this section, we will…
▫ Determine if a given ordered pair is a solution to a
system of linear equations
▫ Use appropriate vocabulary:
▫ consistent system – a system of equation with a
solution
▫ inconsistent system – a system of equation without a solution
▫ dependent equations – equations that are equivalent
(i.e. are the same when graphed)
▫ independent equations –equations that are not equivalent
(i.e. are not the same when graphed)
▫ Solve a system of linear equation by the graphing
method
To solve many problems, we must use two variables and this requires that
we solve a system of equations.
A system of linear equations is two or more linear
equations considered at
the same time.
For any one equation, there are an
infinite number of solutions .
For example, look at the equation
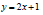
Also consider the linear equation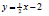 
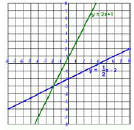
Solution to the system :
Each of these equations has an infinite number of
solutions, however,
there is only ONE solution that works for both equations!
We will be checking our solution by ensuring that it
satisfies both of the
linear equations in the system.
Example: Perform a check to ensure that (-2, -3) satisfies
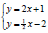
Example: Determine if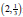 
is a solution of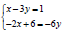 
There are three possibilities for the manner in which the graphs of two linear
equations could meet. The lines could…
▪ Consistent system – a system of equation with a
solution
▪ Inconsistent system – a system of equation without a solution
▪ Dependent equations – equations that are equivalent
▪ Independent equations – equations that are not equivalent
We will be solving systems of linear equations
(and checking those solutions)
• graphically
• algebraically
• by substitution
• elimination
Solving Systems of Linear Equations Graphically
1. Graph each line using a straight-edge (use the slope- intercept method )
2. Find the coordinate of the solution to the system
3. Check your result in BOTH equations
Example: Solve the system of linear equations by graphing.
(+ check)
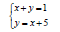
Is the system consistent or inconsistent?
Are the equations dependent or independent?
Example: Solve the system of linear equations by graphing.
(+ check)
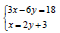
Is the system consistent or inconsistent?
Are the equations dependent or independent?
Example: Solve the system of linear equations by graphing.
(+ check)
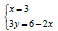
Is the system consistent or inconsistent?
Are the equations dependent or independent?
Example: Solve the system of linear equations by graphing.
(+ check)
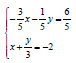
Is the system consistent or inconsistent?
Are the equations dependent or independent?
Example: Solve the system of linear equations by graphing.
(+ check)
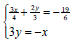
Is the system consistent or inconsistent?
Are the equations dependent or independent?
Example: The following graph illustrates the supply and
demand of dog food.
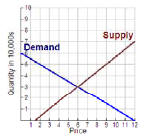
a) As the price of the dog food increases,
what happens to the supply?
b) As the price of dog food increases, what
happens to the demand?
c) For what price will the supply equal
demand?
d) How many items will be supplied at this
price?
Independent Practice
You learn math by doing math. The best way to learn math is to practice,
practice, practice. The assigned homework examples provide you with an
opportunity to practice. Be sure to complete every assigned problem (or more
if you need additional practice ). Check your answers to the odd-numbered
problems in the back of the text to see whether you have correctly solved each
problem; rework all problems that are incorrect.
Read Section 4-1
Homework: pages 185 – 186 (all odds 1-35 and 51)
