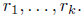All polynomials here have integer coefficients.
Example: Long Division of polynomials (for a linear
divisor ). The long division
x4 - x3 + 2x divided by x - 3,
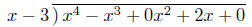
has a quotient x3 + 2x2 + 6x + 20 and a remainder 60.
Theorem For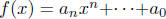 
and
an integer b, we can write f(x) = (x - b)g(x)+c
where g is a polynomial with degree g = degree f - 1 and c is an integer.
Proof. By induction on the degree of f. The result
is clearly true when the degree
of f is zero . Suppose that the assertion holds when the degree of f is less than
n and
now take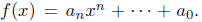 
Now the nth degree coefficient of f
is a n which
is the same as the nth degree coefficient of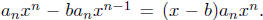 
Hence
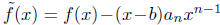has degree less than n. By induction,
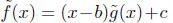
where the degree of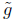 
is less than n. Then
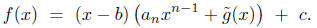
By induction, the result holds for all polynomials f.
Definition. The polynomials
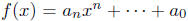and
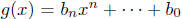are
congruent as polynomials modulo m (written f ≡ g (poly modm)) if
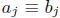(mod m)
for each j with 0 ≤ j ≤ m. Another way of saying this is f(x) - g(x) = mh(x)
where
h is a polynomial with integer coefficients.
Example. x2 + x - 12 ≡ x2 + x + 2 (poly mod 7).
However, although by Fermat’s
theorem we have x7 ≡ x (mod 7) for every x, we do not have x7 ≡ x(poly mod 7).
Definition. For f as above, the degree of f modulo
m is the largest j such that
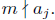
If f is congruent to zero modulo m then the degree is undefined.
Lemma If
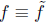(poly mod m) and
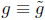(poly modm) then
(poly mod m)
and
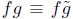(poly mod m). Also
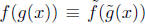(poly mod n) as was noted by a
member of the audience. If m = p is prime then the degree of fg modulo p is the
degree of f modulo p plus the degree of g modulo p.
Theorem. Let p be prime and let f(x) be a
polynomial which is not congruent to
zero as a polynomial modulo p.
(a). There exist integers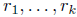
and a polynomial g(x), such that g has no roots
modulo p and
(*)
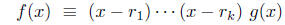(poly mod p):
(b). Moreover
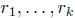are precisely the roots of f (possibly repeated more than
once), and so by comparing the degree modulo p of both sides, the number of
roots of
f is at most n.
Example. Consider x4 -1 modulo 5. By Fermat, the
roots are 1; 2; 3; 4 modulo 5. By
the Theorem
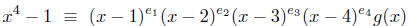(poly mod 5);
where the exponents
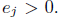By comparing degrees and the coefficient of x4 on both
sides,
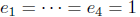and g(x) = 1 and
x4 - 1 ≡ (x - 1)(x - 2)(x - 3)(x - 4) (poly mod 5):
Proof of the Theorem. (a). We prove this by
induction on the degree of f. Suppose
it holds when the degree of f is less than n, and now take f whose degree is
precisely
n. If f has no root modulo p then we can take g = f and no rs. If f has a root r
modulo p. Then by long division we can write
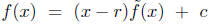
where the degree of
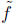is n - 1. Then plugging in x = r we get
0 ≡ f(r) ≡ c (mod p)
and so
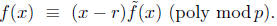
By applying the inductive hypothesis to
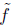we get (*) for f. By induction we are done.
(b). Clearly
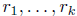are roots of f modulo p and if a is not one of the
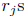modulo p
we have
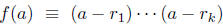g(a) (mod p)
which is a product of non -zero elements modulo p and hence
non-zero modulo p. This
shows that the roots modulo p are precisely
