Graphs of Fundamental Functions
The following are fundamental functions whose stated
properties and graphs you must
know.
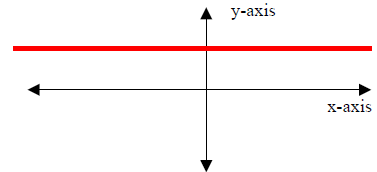
1. The Constant Function
y = f(x) = c
Properties :
(I) Domain: x∈(- ∞, ∞)
(II) Range: y∈{c}or y = c.
(III)
y- intercept : (0, c)
x- intercept : None except for y = f(x) = 0 (In this case the
x-axis is the graph)
(IV) Constant over x∈(- ∞, ∞), that is, always constant
(V) Symmetry: Even (y-axis symmetry)
(VI) End Behavior:
As x → - ∞, y = c
As x → ∞, y = c
(VII) No asymptote. |
 |
| |
|
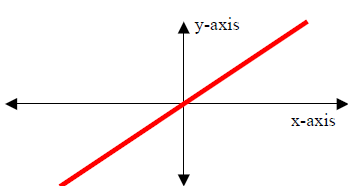
2. The Identity Function
y = f(x) = x
Properties :
(I) Domain: x∈(- ∞, ∞)
(II) Range: y∈(- ∞, ∞).
(III) y- intercept : (0,0); x- intercept : (0,0)
(IV) Increasing over x∈(- ∞, ∞), that is, always increasing
(V) Symmetry: Odd (origin symmetry)
(VI) End Behavior:
As x → - ∞, y → - ∞
As x → ∞, y → ∞
(VII) No asymptote. |
 |
| |
|
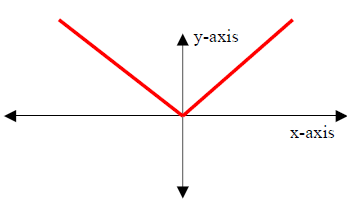
3. The Absolute Value Function
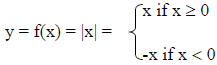
Properties:
(I) Domain: x∈(- ∞, ∞)
(II) Range: y∈[0, ∞).
(III) y-intercept: (0,0); x-intercept: (0,0)
(IV) Decreasing over x∈(- ∞, 0). Increasing over x∈(0, ∞).
(V) Symmetry: Even (y-axis symmetry)
(VI) End Behavior:
As x → - ∞, y → ∞
As x → ∞, y → ∞
(VII) No asymptote. |
 |
| |
|
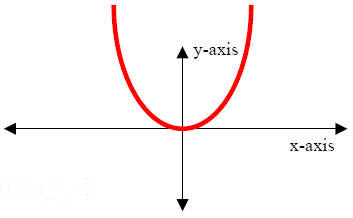
4. The Square Function
y = f(x) = x2
Properties:
(I) Domain: x∈(- ∞, ∞)
(II) Range: y∈[0, ∞).
(III) y-intercept: (0,0); x-intercept: (0,0)
(IV) Decreasing over x∈(- ∞, 0). Increasing over x∈(0, ∞).
(V) Symmetry: Even (y-axis symmetry)
(VI) End Behavior:
As x → - ∞, y → ∞
As x → ∞, y → ∞
(VII) No asymptote. |
 |
| |
|
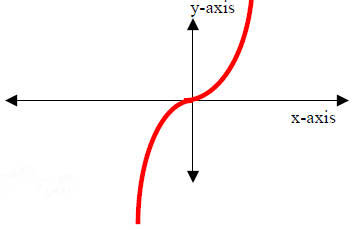
5.The Cube Function
y = f(x) = x3
Properties:
(I) Domain: x∈(- ∞, ∞)
(II) Range: y∈(- ∞, ∞).
(III) y-intercept: (0,0); x-intercept: (0,0)
(IV) Increasing over x∈(- ∞, ∞); that is, always increasing
(V) Symmetry: Odd (origin symmetry)
(VI) End Behavior:
As x → - ∞, y → - ∞
As x → ∞, y → ∞
(VII) No asymptote. |
 |
| |
|
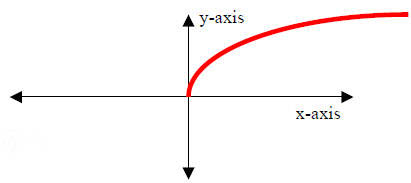
6. The Square - Root Function
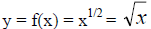
Properties:
(I) Domain: x∈[0, ∞)
(II) Range: y∈[0, ∞).
(III) y-intercept: (0,0); x-intercept: (0,0)
(IV) Increasing over x∈(0, ∞).
(V) Symmetry: None
(VI) End Behavior:
As x → 0+, y → 0
As x → ∞, y → ∞
(VII) No asymptote. |
 |
| |
|
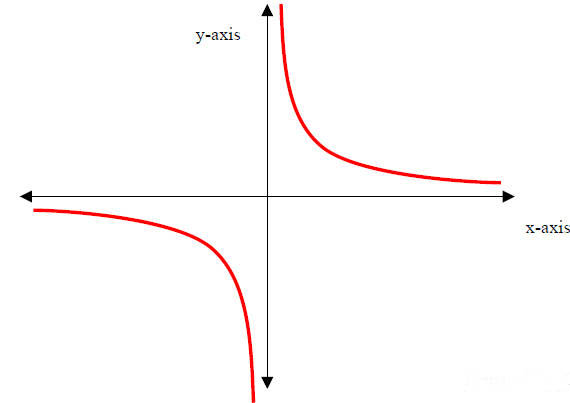
7. The Reciprocal Function
y = f(x) = 1/x
Properties:
(I) Domain: x∈(- ∞, 0) ∪ (0, ∞). That is, all real numbers except x = 0.
(II) Range: y∈(- ∞, 0) ∪ (0, ∞). That is, all real numbers except y = 0.
(III) y-intercept: None; x-intercept: None
(IV) Decreasing over x∈(- ∞, 0) and over x∈(0, ∞).
(V) Symmetry: Odd (origin symmetry)
(VI) End Behavior:
As x → - ∞, y → 0;
As x → 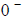 (approaches 0 from the left), y → - ∞ (approaches 0 from the left), y → - ∞
As x → 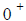 (approaches 0 from the right), y → ∞ (approaches 0 from the right), y → ∞
As x → ∞, y → 0
(VII) Vertical asymptote: x = 0 (y-axis); Horizontal asymptote:
y = 0
(x-axis) |
 |
| |
|
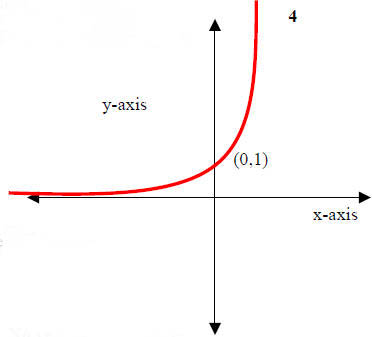
8. The Exponential Function
y = f(x) = exProperties:
(I) Domain: x∈(- ∞, ∞)
(II) Range: y∈(0, ∞).
(III) y-intercept: (0,1); x-intercept: None
(IV) Increasing over x∈(- ∞, ∞); that is, always increasing
(V) Symmetry: None
(VI) End Behavior:
As x → - ∞, y → 0
As x → ∞, y → ∞
(VII) Horizontal asymptote: y = 0 (the x-axis). No vertical asymptote. |
 |
| |
|
|
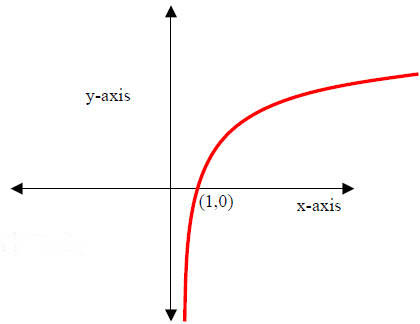
9. The Natural Logarithm Function
y = f(x) = ln(x)
Properties:
(I) Domain: x∈(0, ∞)
(II) Range: y∈(- ∞, ∞).
(III) y-intercept: None; x-intercept: (1,0)
(IV) Increasing over x∈(0, ∞); that is, always increasing
(V) Symmetry: None
(VI) End Behavior:
As x → 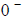 , y → - ∞ , y → - ∞
As x → ∞, y → ∞
(VII) Vertical asymptote: x = 0 (the y-axis). No horizontal asymptote. |
 |
Note:
y = ex and y = ln(x) are inverse functions.
If two functions are inverses of each other then the domain of one is the range
of the
other and vice versa. For example, if (2, -3) is a point on a function, then
(-3, 2) is a point
on its inverse.
To get the graph of the inverse of a function from the graph of the function,
simply reflect
the graph about the line y = x.
So if you start out with y = ex , you can get the graph of y = ln(x), simply
reflect the
graph of y = ex about the line y = x.
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
January 2nd
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
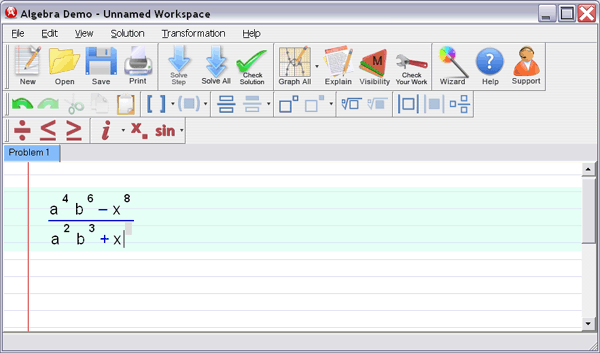
Step 2 :
Let Algebra Helper solve it:
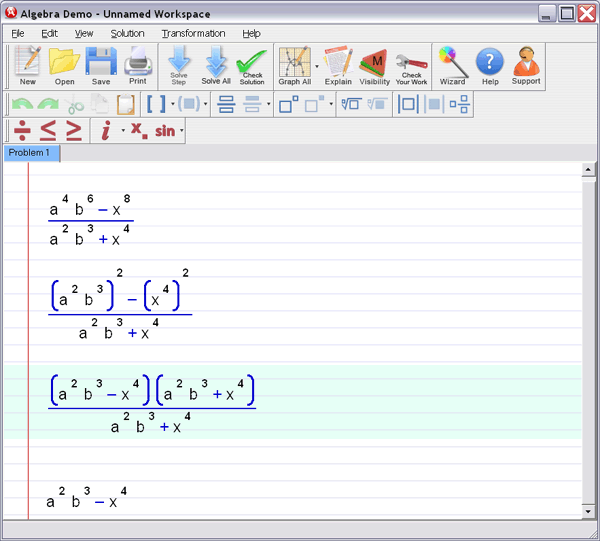
Step 3 : Ask for an explanation for the steps you don't understand:
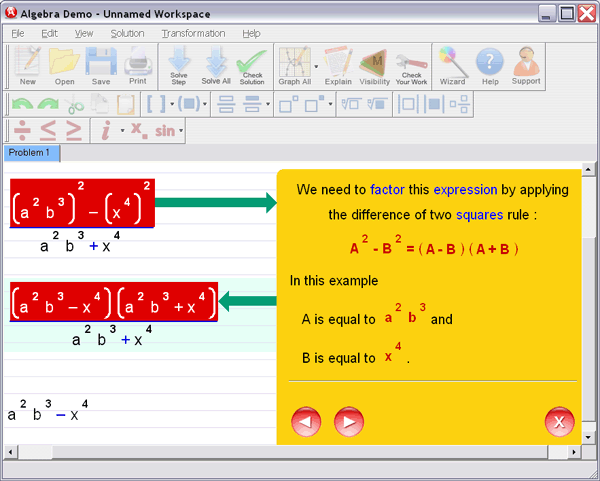
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



