Midterm Exam Number Two Review

• Be able to find a linear formula from a verbal description. Look for words like “...is a
linear function of...”, “...has a straight line graph...”, “items sell for $0.15 each” (tells
you TR is linear), “it costs you $10 to make each item” (tells you TC is linear).

• Given a formula for distance , you should be able to find formulas for average trip
speed and average speed over an interval of a specified length (see WS 12). You
should be able to do this in other contexts as well.

e.g., Given the total amount of water in a vat, W(t), find formulas for overall and
incremental rates of change . Or, given the TC, find formulas for AC and MC.

• Given a formula for price per item as a function of q, you should be able to find
formulas for TR(q) and MR(q):

TR(q) = p · q

MR(q) = TR(q + 1)− TR(q)

(see WS 13)

• If you have formulas for MR and MC and you want the quantity that maximizes
profit, you should be able to set MR = MC and solve for q . Round up to the nearest
whole number of items (being careful if q is measured in hundreds, e.g., q = 2.13 is
a whole number of items .) If you get two positive quantities at which MR = MC,
remember profit is maximized at a transition from MR > MC to MR < MC.

• You should know when and how to apply the vertex formula /method. Suppose f(x) =
ax² + bx + c with a < 0. Then the vertex formula 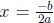gives the value of x that
maximizes f(x). To find the maximum value of f(x), you can plug 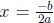  back into
f(x).

Typical questions:

– Find the time/quantity at which (some quadratic function ) is largest/smallest/
lowest /highest/maximized/minimized.

– Find the largest/smallest/ lowest /highest/maximum/minimum value of (some
quadratic function).

Special note: If profit is a quadratic function and you use the vertex formula to
maximize profit and 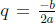is not a whole number, then you should round to the
nearest whole number quantity.

• The vertex formula can also give information about when a quadratic function is
increasing/decreasing. In particular, if you’re asked to find an interval on which a
function is increasing, draw a rough sketch.

e.g.:
f(x) = −3x² + 12x − 19 opens down, vertex at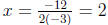

so f(x) increases from x = 0 to x = 2, for instance

As opposed to g(x) = −3x + 4 which is always decreasing.

• Know when and how to apply the quadratic formula. Use the quadratic formula to
solve an equation of the form ax² + bx + c = 0.

Example: Suppose profit is given by

P(q) = −3q² + 12q − 19.

P(q) is a quadratic function but it is not a quadratic equation. However if we want to
know what quantity makes a profit of $15, then we can solve the quadratic equation

−3q² + 12q − 19 = 15

by rewriting it as

−3q² + 12q − 34 = 0

and applying the quadratic formula.

• You should understand how TR, TC and profit can be read as areas of rectangles
under the price and AC per item functions. (WS 15)

• You should be able to answer questions about TR, TC, and profit given the formulas
for p and AC. (WS 15)

• You should have a clear understanding of how all of the following are related:

– TR and MR and AR and p
– TR(q) = p · q, MR(q) = TR(q + 1) − TR(q),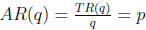

– TC, FC, VC, AC, AVC, MC:

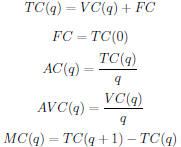
• You should understand that breakeven price is

– the smallest value of AC (so if AC is a quadratic function of q this is the “y”-
coordinate of the vertex of AC)

– the “y”-coordinate of the point where AC and MC intersect

• You should be able to determine distance travelled from informatino about speed. In
particular, if speed is a known linear function of time, then you should be able to
describe distance as a quadratic function of time, and answer questions about those
functions. (WS 17)