The area between the curves y = f(x) and y = g(x) and
between x = a and x = b is
An analogous formula holds for the area between the curves
y = c and y = d and x = f(y) and x = g(y):
For a solid S lying between x = a and x = b with
cross-sectional area function A(x) (A continuous),
the volume of S is
Again, an analogous formula holds for the volume of a
solid S lying between y = c and y = d with
cross-sectional area function A(y) (A continuous). In this case,
1.
2.
3. (6.1.50) Find the number a such that the line x = a
bisects the area under the curve y = 1/(x^2)
for 1≤x≤4. Also, find the number b such that the line y = b bisects the same
area.
Solution : We want our line x = a to split our areas. That
is, we want an a so that 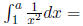
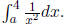
Taking the integrals, we find 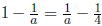 Solving for a ,
we find that
Solving for a ,
we find that 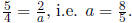
For the second part, we want to split the areas using a
horizontal line y = b. A horizontal line
will give us a wedge above the line and a region below that includes a rectangle
sitting below the
line y = 1/16. The area of the lower region is 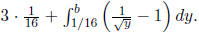 The
first term comes
The
first term comes
from the rectangle of length 3 between 1 and 4 and height 1/16. The second terms
comes from
determining the area between the curve 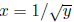 and x =
1. The upper region has area given by
and x =
1. The upper region has area given by
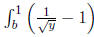 dy. We set these two equal to each other and
integrate to get
dy. We set these two equal to each other and
integrate to get
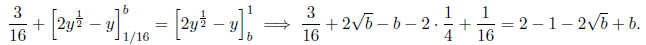
We simplify this to get 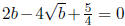 To solve for b , we set c^2 = b and consider
To solve for b , we set c^2 = b and consider 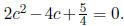
We solve for c using the quadratic formula to get
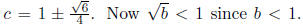 Thus
Thus
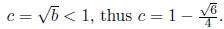 Squaring this we get
Squaring this we get
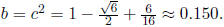
Solution: The solid looks like the space between a
funnel and a cylinder. We split this solid
into two different regions : the lower one consists of a cylinder with a hole and
the upper region
is a triangle rotated around the line x = 1. The lower region has
cross-sectional area
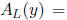
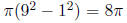 and the
upper region has cross-sectional area
and the
upper region has cross-sectional area 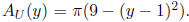
Then we find
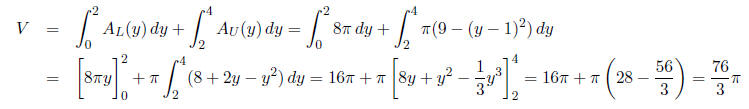
5. Suppose 2≤f(x)≤4 for all x. Which of the following is
false:
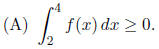
(B) The antiderivative of f is always positive .
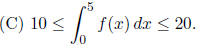
(D) The antiderivative of f is always negative .
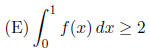
Solution: (A) is true since f(x)≥2 for all x. (C) is true
since 2≤f(x)≤4 implies that
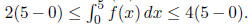 (E) is true since
(E) is true since
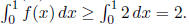 For (B) and (D), note
For (B) and (D), note
that an antiderivative of f is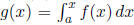 by the
Fundamental Theorem of Calculus. Since
by the
Fundamental Theorem of Calculus. Since
f(x) > 0, g(x) > 0 for any x. Thus (B) is true while (D) is false. Hence the
answer is (E).