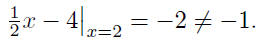Functions & First Degree Curves
Solutions to Exercises
9.1. Solutions:
(a) Given y = 5x + 1, write x as a function of y.
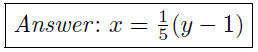
(b) Given 4x − 2y = 1, write y as a function of x.
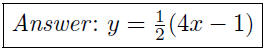
(c) Given 4x − 2y = 1, write x as a function of y.
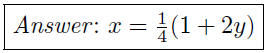
(d) Given 2w + 3s^3 = 3, write s as a function of w.
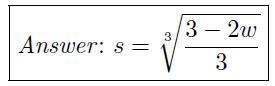
(e) Given 2w + 3s^3 = 3, write w as a function of s.
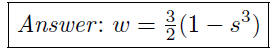
9.2. Solution: As the first step, find surface area, S, as a function of
x. Why? Because its easy!
S = 6x^2
But we don’t want this. We want x as a function of S. No problem:
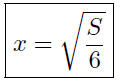
Now, given that we have a cube with surface area of S = 24, we can
now easily compute the length of the common side :
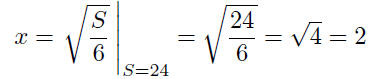
(Here, the vertical bar, |, is the so-called, evalutional notation—a standard
way of conveying the idea that we are substituting a particular
value into a formula.) Thus,
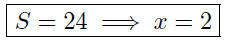
9.3. Solution: It is well know that V = 4/3πr^3. This represents V as
a function of r. We want r as a function of V . Thus,
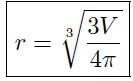
Given the volume, V , this formula lends itself to the easy calculation
of the radius.
9.4. Solution: It is well known that S = 4πr^2. This represents S as
a function of r. We want r as a function of S. Thus,
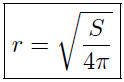
Given the surface area, S, this formula lends itself to the easy calculation
of the radius.
9.5. Solution to (a) From Part (f), we have C = 2πr. This defines C
as a function of r; what this means is that this equation is designed
to give back certain information, C, given that you know the value of
r—and we do.
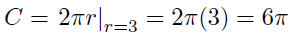
A circle of radius r = 3 has a circumference of C = 6π.
Solution to (b) From Part (g), we have r = C/2π. This defines r as a
function of C.
Now we are given that C = 20π; therefore,
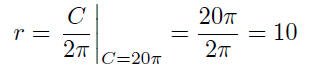
The radius of a circle with circumference C = 20π is r = 10
9.6. I cannot justify it in your own mind, only in mine.
9.7. For each y we can have at most one x; therefore, if we draw a
horizontal line at position y on the y-axis, the line should intersect
the graph of x = g(y) in at most one location.
This is the horizontal analog to the Vertical Line Test. We can formulate
this into a test procedure.
Horizontal Line Test:
A curve C in the xy-plane defines x as a function of y if it
is true that everyhorizon tal line intersects the curve at no
more than one point.
9.8. Solutions:
(a) P(3, 1) and Q(4, 5)
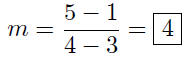
(b) P(−2,−3) and Q(0, 2)
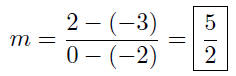
(c)
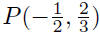and Q(−3, 2)
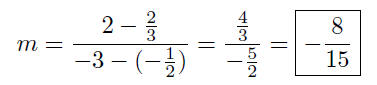
(d) P(2, 1) and the origin, i.e., take Q(0, 0).
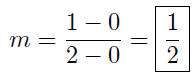
9.9. Solution: Substituting into equation (8), to obtain
Given: P(−4,−1) and Q(5, 1)
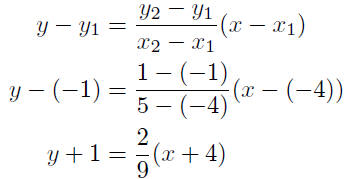
or,
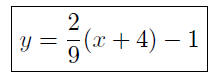
9.10. Solution: The y- intercept is found by putting x = 0 and solving
for y:
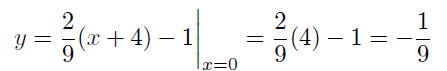
The y-intercept is
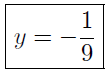
The x-intercept is found by putting y = 0 and solving for x :
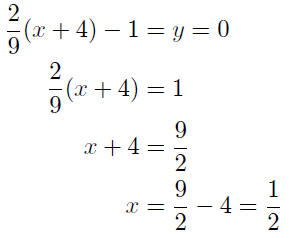
The x-intercept is
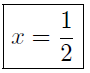
Thus, this line crosses the x-axis at x = −1/9 and crosses the y-axis
at y = 1/2. It is now a trivial matter to draw the graph of the line.
9.11. Solution: The x-intercept is x = 2 and the y-intercept is y =
5; this means the line passes through the points P(2, 0) and Q(0, ).
Therefore,
Given: P(2, 0) and Q(0, 5)
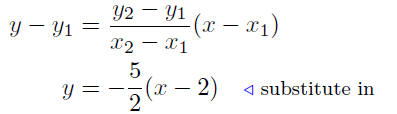
Now we try to put the last equation in the prescribed form .
9.12. Solution: The solution follows along the same lines as the
previous exercise.
Given: P(a, 0) and Q(0, b)
 |
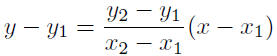two-point form |
 |
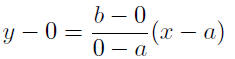substitute in |
 |
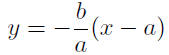simplify |
Now we try to put the last equation in the prescribed form.
 |
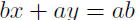clear fractions and expand |
 |
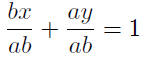divide by ab |
 |
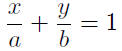the required equation! |
9.13. Solution: We use the two-intercept form:
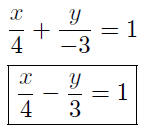
That was quick!
9.14. Solution: We use equation (10):
Given: m = −2 and P(3,−6)
| y − y1 = m(x − x1) |
equation (10) |
| y − (−6) = −2(x − 3) |
substitute |
| y + 6 = −2(x − 3) |
a rewrite |
| y = −6 − 2(x − 3) |
write as a function of x |
| y = −2x |
combine |
Presentation of Answer: y = −2x
The choice of a second point is entirelyup to you. I’ll take x = 1.
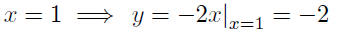
Thus the point Q(1,−2) lies on the equation. Now plot the given point
P(3,−6) and the computed point Q(1,−2), and draw a straight line
through these two points.
9.15. Solution: We use equation (10):
Given: m = −1/2 and P(−2,−9)
 |
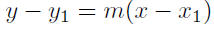equation (10) |
 |
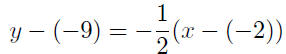substitute |
 |
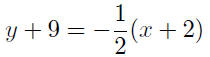a rewrite |
 |
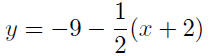write as a function of x |
 |
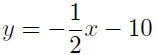combine |
Thus, y = −1/2x − 10 is the equation of the target line written as a
function of x. It was requested that the answer be written in the form
of x as a function of y.
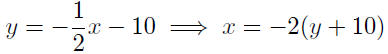
Presentation of Answer: x = −2(y + 10)
9.16. Solution: We are given the slope, m = 6, and the y-intercept;
this is a job for the slope-intercept form of the equation of a line.
Given: m = 6 and b = −1
| y = mx + b |
slope-intercept form |
| y = 6x − 1 |
substitute and done! |
Presentation of Answer: y = 6x − 1
Comments: Be neat and organized in your presentation. It is important
to acquire a mathematical literacy . It is more difficult for me to
type out a neat, well-organized presentation than it is for you to write
one out.
9.17. Solution: This is a job for the slope-intercept form of the equation
of a line.
Given: m = −2 and b = 6
| y = mx + b |
slope-intercept form |
| y = −2x + 6 |
substitute and done! |
Presentation of Answer: y = −2x + 6
9.18. Solution: We are given two points. We could use the two-point
form, or we could (1) compute the slope, then (2) use the point-slope
form. I’ll take the latter tack:
1. Compute the slope.
Given: P(3, 1) and Q(4, 5),
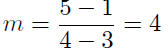
2. Now use the point- slope form .
Given/Known: P(3, 1) and m = 4,
| y − y1 = m(x − x1) |
point-slope form |
| y − 1 = 4(x − 3) |
substitute |
| y = 1 + 4x − 12 |
expand |
| y = 4x − 11 |
combine |
Presentation of Answer: y = 4x − 11
9.19. Solution: Given P(−2,−5) and m = 1/2
 |
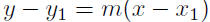point-slope form |
 |
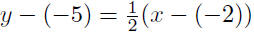substitute |
 |
|
 |
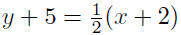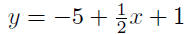expand |
 |
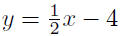combine |
Presentation of Answer:
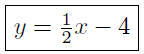
9.20. Solution:
(a) Compute the slopes of each of these two lines.
• The slope of the line y = 3x − 1 is m = 3, the coefficient
of the x term.
• The slope of the line y = 1− x is m = −1, the coefficient
of the x term.
(b) State the y-intercepts of each line.
• The y-intercept of the line y = 3x − 1 is b = −1, the
constant term.
• The y-intercept of the line y = 1−x is b = 1, the constant
term.
9.21. Solution: The point of intersection (x, y) satisfies both equations.
Generally, to find the point of intersection we equate the y-values:
| 3x −1 = y = 1− x |
equate ordinates |
| 3x − 1 = 1 − x |
eliminate redundant notation |
4x = 2
x = 1/2 |
|
The two lines intersect when the abscissa is x = 1/2 . But
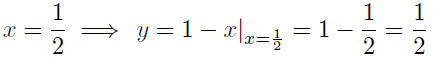
Thus, the two lines intersect at
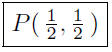
Draw these two lines on the same sheet of paper in order to see the
point of intersection. (Or, have your student held graphing calculator
do it for you.)
9.22. Solution: We simplyput each in the slope-intercept form.
(a) Find the slope and y-intercept of the line 5x + 3y − 1 = 0.
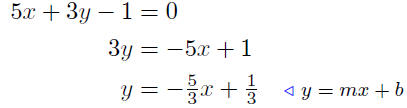
This line has slope m = −5/3 and y-intercept of y = 1/3.
(b) Find the slope and y-intercept of the line −3x + 12y+13 = 0.
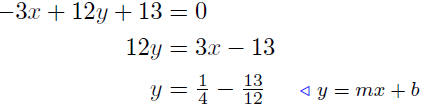
This line has slope m = 1/4 and has y-intercept of y = −13/12 .
(c) Find the slope and y-intercept of the line x − y = 0.
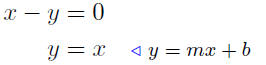
This line has slope m = 1 and y-intercept of y = 0.
9.23. Solution: Trivial. The keyp oint is finding an additional point
on the each line—that’s done using the equation.
9.24. Solution: There are two solutions.
The Quick Solution: Note that the two given points, (−4, 1) and (5, 1),
have the same ordinate; therefore, this is a horizontal line. Its equation
is
y = 1
The Long Solution: The long solution uses standard methods .
Calculate Slope:
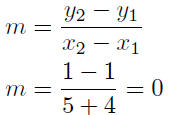
Point-Slope Form:
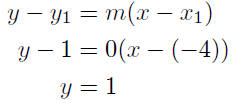
Again we arrive at the conclusion that y = 1 is the equation of the
line. Which way did you do it?
9.25. Solution: The calculation of the intercepts from the general
form is very quick. The graphing is trivial so I’ll not bother to prepare
the graphs for you.
(a) Find the intercepts of 3x + 4y = 24.
3x + 4y = 24
y-intercept: Put x = 0
4y = 24
y = 6 |
x-intercept: Put y = 0
3x = 24
x = 8 |
Presentation of Answer: The x- and y- intercepts are, respectively,
x = 8, y = 6 .
The solutions to the other two parts are on the next page. Given that
you have looked at the solution to part (a), you may want to revise
your solutions to parts (b) and (c) before looking.
(b) Find the intercepts of 5x − 2y = 10.
5x − 2y = 10
y-intercept: Put x = 0
−2y = 10
y = −5 |
x-intercept: Put y = 0
5x = 10
x = 2 |
Presentation of Answer: The x- and y- intercepts are, respectively,
x = 2, y = −5 .
(c) Find the intercepts of x − 2y = 1.
x − 2y = 1
y-intercept: Put x = 0
−2y = 1
y = −1/2 |
x-intercept: Put y = 0
x = 1 |
Presentation of Answer: The x- and y- intercepts are, respectively,
x = 1, y = −1/2 .
The graphing of these equations is left to the student—that’s you.
9.26. Solutions:
(a) Find the point of intersection: x − y = 1 and x + y = 1.
Solution: Begin by solving for y in each equation.
| x − y = 1 |
given |
x + y = 1 |
given |
| y = x − 1 |
solve for y |
y = 1− x |
solve for y |
Now equate ordinates
x −1 = y = 1− x
and solve for x
| x − 1 = 1 − x |
from above |
| 2x = 2 |
|
| x = 1 |
solved! |
Now, substitute the value of x = 1 into any of the two equations
to get y = 0.
Presentation of Answer: Point of intersection is P(1, 0)
(b) Find the point of intersection: x − 3y = 1 and 2x − y = 1.
| x − 3y = 1 |
given |
2x − y = 1 |
given |
| y = 1/3(x − 1) |
solve for y |
y = 2x − 1 |
solve for y |
Now equate ordinates
1/3(x − 1) = y = 2x − 1
and solve for x
| 1/3(x − 1) = 2x − 1 |
from above |
| x − 1 = 6x − 3 |
clear fractions |
| x = 2/5 |
solve for x |
Now, substitute the value of x = 2/5 into any of the two equations to get y =
−1/5
Presentation of Answer: Point of intersection is
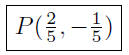
(c) Find the point of intersection: 4x − 2y = 7 and y = 2x + 1.
| 4x − 2y = 7 |
given |
y = 2x + 1 |
given |
| y = 1/2(4x − 7) |
solve for y |
|
|
Now equate ordinates
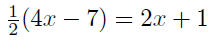
and solve for x
| 1/2(4x − 7) = 2x + 1 |
from above |
| 4x − 7 = 4x + 2 |
clear fractions |
| −7 = 2 |
substract 4x from both sides |
Conclusions: The last equation has no solution—the x’s have
been totally eliminated. This means that there are no x’s that
satisfy the equation 1/2(4x − 7) = 2x + 1; hence, these two lines
do not intersect—they are in fact parallel.
(d) Find the point of intersection: 6x + y = 3 and x + y = 2.
| 6x + y = 3 |
given |
x + y = 2 |
given |
| y = −6x + 3 |
solve for y |
y = 2− x |
solve for y |
Now equate ordinates
−6x + 31 = y = 2− x
and solve for x
| −6x+3 = 2 − x |
from above |
| −5x = −1 |
|
| x = 1/5 |
|
Now, substitute the value of x = 1/5 into any of the two equations
to get y = 9/5
Presentation of Answer: Point of intersection is
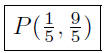
9.27. Solution: This problem is no different from the problems seen
earlier (See, e.g., Exercise 9.14); the only difference is that we get
our slope from the given line.
The slope of the line y = 2x−1 is m = 2. We want to construct a line
parallel to this line, so it too should have a slope of m = 2; however,
our line is required to pass through the point P(2, 7):
Given: m = 2 and P(2, 7)
| y − y1 = m(x − x1) |
point-slope form |
| y − 7 = 2(x − 2) |
substitute |
| y = 2x + 3 |
|
Presentation of Answer: The line that is parallel to the line y = 2x−1
and passes through the point P(2, 7) is
y = 2x + 3
9.28. Solution: Same problem as just solved, the only difference is
we have to work a little harder to get the slope.
Given line: 5x + 4y = 12
4y = −5x + 12
y = −5/4x + 12
The slope of the given line is m = −5/4
Given: m = −5/4 and P(−3,−1)
| y − y1 = m(x − x1) |
point-slope form |
 |
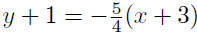substitute |
 |
|
 |
|
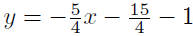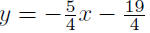Presentation of Answer:
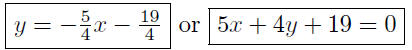
9.29. When m1 = 0 (m2 = 0), then line
(resp.
)
is a horizontal
line. In this case, only vertical lines are perpendicular to it!
Typically, horizontal lies have equation y = a, and vertical lines have
equation x = b. It is veryeasy to determine whether anyline is perpendicular
to either a horizontal line or a vertical line.
9.30. Solution: The slope of the given line is mgiven = 5 and so the
slope of the line we are trying to construct has slope
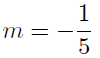from (14)
We now go into our point-slope mode (our most powerful
mode of
thought): Given m = −1/5 and P(3, 4),
 |
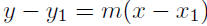point-slope form |
 |
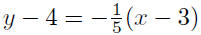substitute |
 |
|
 |
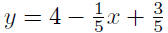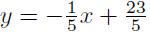slope-intercept |
Presentation of Solution: The desired line is
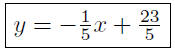
9.31. Solution: The given line 6x + 2y = 1 can be
rewritten in the
slope-intercept form as y = −3x + 1/6. Therefore, the given line has
slope of mgiven = −3, so the line we are trying to construct
has slope
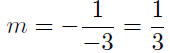from (14)
We use the point-slope form: Given m = 1/3 and P(−5, 3),
| y − y1 = m(x − x1) |
point-slope form |
| y −3 = 1/3(x + 5) |
substitute |
| y = 3+ 1/3x + 5/3 |
|
| y = 1/3x + 14/3 |
slope-intercept |
Presentation of Solution: The desired line is
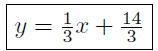
9.32. Solution to (a) Let
denote the given line y = 2x + 4. Here
is an obvious sequence of steps.
1. Compute the equation of the line
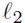that passes through the
given point, P(−1,−1) and is perpendicular to the given line,
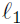: y = 2x + 4. Draw a picture of this line.
2. Find the point of intersection of the two lines
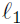, the given line,
and 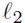, the line perpendicular to the
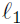, as developed in Step 1.
3. Having found the point of intersection between
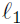and ,
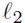call
this point Q, the desired distance is d(P,Q), the distance between
point P and Q.
Carryout this game plan before looking at the solution to
part (b)
on the next page.
Step 1: Find the equation of the line perpendicular to the
given line
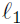and passing through the given point. The
equation of that line is
y + 1 = −1/2(x + 1)
or,
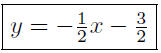
Verify these calculations if you missed this step.
Step 2: Find the point of intersection between
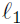: y = 2x + 4 and
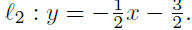
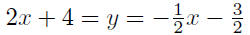
therefore,
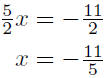
Verify all details. Substitute this value of x into either
of the two
equation to obtain
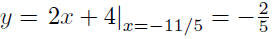
Thus, the point of intersection between
and is
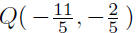
Step 3: Find the distance between P and Q.
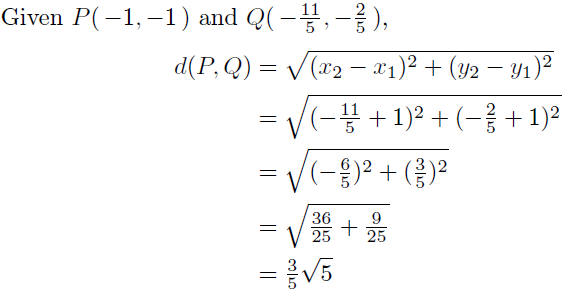
Presentation of Answer: The distance between the point
P(−1,−1)
and the line y = 2x + 4 is
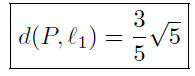
Comments: That was a multi step problem ! Each step,
however, was
a problem type examined earlier. In mathematics, we try to outline
in our minds a plan of attack, then try to carryout the plan—being
ready and willing to modify our plan or our thinking at all times.
This problem can be carried out in the abstract to obtain
a nice little
formula.
For those who want to do more. Problem: Find a
general formula
for the problem of finding the distance from a given point P(x0, y0)
and a given line y = mx + b.
Solution: Just carryout the game plan as outlined in part
(a).
Solutions to Examples
9.1. Solution:
| y = 3x − 1 |
given |
| 3x −1 = y |
transpose |
| 3x = y + 1 |
|
| x = 1/3(y + 1) |
solve for x |
Thus, we have written x as a function of y:
x = 1/3(y + 1)
9.2. Solution: To calculate slope, you take the difference
in the ordinates
(the second coordinates) and divide by the difference in the
abscissas (the first coordinates) being sure to subtract in the same
order in both numerator and denominator .
Given: P(−1, 3) Q(4, 1)
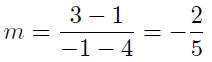
The slope of the line is m = −2/5
9.3. Solution: We can substitute directly in to equation
(8). I shall
consider (x1, y1) = (−2, 4) and (x2, y2) = (6, 9).
Thus, from (8) we have
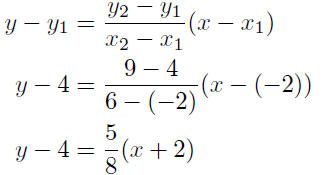
An equation for this line is
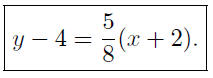
If we write this equation so that y is a function of x we
get
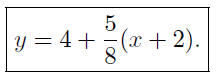
9.4. Solution: The equation of the line obtained in
Example 9.3 is
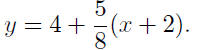
Find the y-intercept: The y-intercept is the point on the
y-axis at
which the line crosses the y-axis. Characteristic of points on the y-axis
is that the x-coordinates are equal to zero. Therefore, to answer
the question we seek the point on the line for which the x-coordinate
is zero.
Set x = 0 in (S-1) to obtain the corresponding value of y:
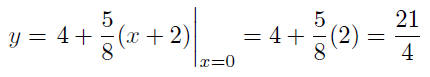
The y-intercept is y = 21/4
Find the x-intercept: The x-intercept is the point where
the line
crosses the x-axis. Characteristic of points on the x-axis is that y = 0.
To find the x-intercept we set y = 0 in equation (S-1) and solve for x.
 |
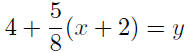Now put y = 0, and . . . |
 |
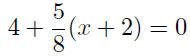solve for x |
 |
|
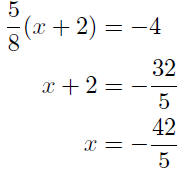Thus the x-intercept is x = −42/5
Find the point on the curve corresponding to x = −2:
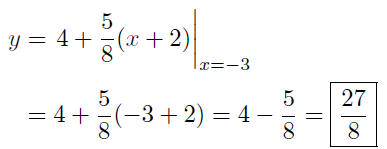
Thus, the point on the curve corresponding to x = −2 is
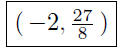
Find the point on the curve corresponding to x = 6:
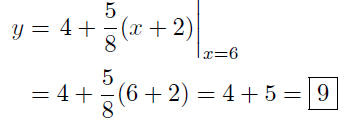
Thus, the point on the curve corresponding to x = 6 is
( 6, 9 )
9.5. Solution: We use equation (10):
Given: m = 5 and P(1, 2)
| y − y1 = m(x − x1) |
equation (10) |
| y − 2 = 5(x − 1) |
substitute |
| y = 2 + 5(x − 1) |
write as a function of x |
| y = 5x − 3 |
combine |
Presentation of Solution: y = 5x − 3
Comments: As you can see the point-slope was indeed a
transitory
form. We used it to obtain an initial formula, then manipulated from
there.
9.6. Solution: We simply put the equation in the
slope-intercept
form.
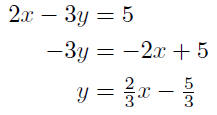
We can now see that the given equation has slope of m =
2/3 and, by
the way, crosses the x-axis at x = −5/3
Important Points
The answer is Yes. When we say that x is a function y we
mean
x = f(y)
for some function f; that is, x is expressible in terms of
y. This means
that corresponding to each y-value (the independent variable), there
is a unique x-value (the dependent variable). In Figure 5, for any
given y, draw a horizontal line at y. Note that this line intersects the
curve in at most one location. This means that for any given y there
corresponds a single x-value. This is the definition of function.
Throughout this discussion, we refer to Figure 6. The
triangle PRQ
is similar to the triangle P'R'Q'. Therefore the ratio of corresponding
sides are equal. Thus,
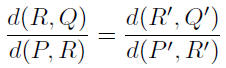
or,
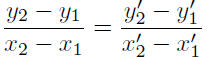
The last set of calculation follow form our discussion of
the distances
between vertically and horizontally oriented points as presented in
Lesson 8.
Note: The above argument is not completely general.
Do you see the
“weakness” of the argument?
The point (2,−1) is not on the line y = 1/2x − 4 because
it does not
satisfy the equation:
