The final exam will be cumulative. However, 3/5 of the
final exam will be on Chapter
11, with 2/5 devoted to things covered in the rest of the course.
No calculators of any kind will be allowed.
Formulas you will be given on the exam (if they are needed):
• The transformation formulas x' = x cosθ + y sinθ and y' = −x sinθ
+ y cosθ , as well
as x = x' cosθ − y' sinθ and y = x' sinθ + y' cosθ .
• The formulas relating A' and C' to A, B, and C when a conic section is rotated
to
remove the xy -term.
Formulas to remember:
• The polar-rectangular transformation formulas:
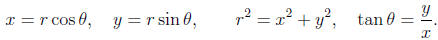
• The most common polar graphs:
– r = c ( circle of radius c centered at the origin)
– θ = c (line of slope m = tan c through the origin)
– r = ±c cosθ (circle of radius c/2 passing through the origin)
– r = c cos nθ for an integer n (rose curves with 2n petals if n is even
and n petals
if n is odd; c is the length of each petal)
–
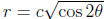(lemniscate, i.e., infinity symbol ; c is the length of the petal)
– r = a + b cosθ (
, i.e., a slug; if a = b, a cardioid, i.e., a
human heart)
– r = cθ or r = ceθ or r = cθ2 or any increasing function of θ (a
spiral expanding
around the origin)
–
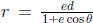(a conic section with a focus at the origin and opening along the
positive x-axis; an ellipse if e < 1, a parabola if e = 1, and a hyperbola if e
> 1)
• Variations and techniques for getting the precise
graphs:
– If the equation only involves cosine, then replacing cosine with sine or
replacing
cosine with negative cosine results in the same shape rotated by some angle.
Thus
you only need to remember the basic forms for the polar curves.
– The effect of changing r = f(θ) to r = cf(θ) is to expand or contract the
entire
graph by a factor of c .
– To plot the standard curves, you only need to know a few special (r, θ) points.
For a circle, lemniscate,
, spiral, or conic section, you can get the
entire
graph just by knowing r at the cardinal angles θ = 0,
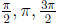. For a rose curve,
it is sufficient just to know which θ gives the maxima, minima, and zeroes of r .
– If you have a polar curve you don’t recognize, you can figure out its graph by
plotting (r, θ) pairs for those values of θ that maximize r, minimize r, or result
in
r = 0. This will always give the essential features of the graph.
– Symmetry can help.
*
If replacing (r, θ) with (r,−θ ) gives the same equation, the graph is symmetric
about the x-axis.
*
If replacing (r, θ) with (r, π − θ) gives the same equation, the graph is symmetric
about the y-axis.
*
If replacing (r,θ ) with either (−r, θ) or (r, θ+π ) gives the same equation, the
graph is symmetric about the origin.
• Slope of the tangent to a parametric equation:
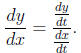
The cancelation of the dt terms makes this formula easy to
remember.
• Concavity of a parametric equation:
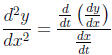
where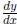 
is computed as
above.
• Slope of the tangent to a polar equation r(θ): Using x = r(θ) cosθ and y =
r(θ)
sinθ
and the product rule , you can derive
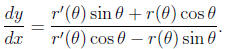
It’s better to derive this formula as needed than to try
to memorize it. NEVER make
the mistake of saying the slope of a polar equation is
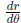. A slope must always be
expressed in rectangular coordinates.
• Arc length of a polar curve r(θ):
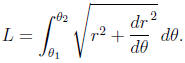
• Area enclosed by a polar curve r(θ):
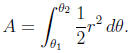
Some subtleties:
– If r ≥ 0 always, then you can find the area by integrating from 0 to 2π .
– If r < 0 for some values of θ, make sure you understand the graph before you
try to integrate. Usually you can use symmetry (for example, when finding area
in a rose, it’s best to find the area in one petal, then multiply by the number
of
petals ). Good bounds to use are consecutive values of θ which make r = 0; for
example, to find the area in cos 3θ , integrate from
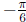to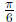 
to get
the area of one
petal, then multiply by three to get the whole area.
– To find the area enclosed by two curves
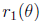and
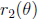, first understand both
graphs. (This is crucial! If you don’t know what the region looks like, you’ll
probably get the wrong answer.) Find the angles of intersection by setting
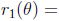
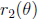, then compute 
• Conic section formulas in rectangular coordinates
(oriented along x-axis):
– Ellipse: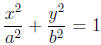
, with a > b. Foci at (c, 0) and
(−c, 0), where c2 = a2 − b2.
If the ellipse has b > a, then the foci are at (0, c) and (0,−c), where c2 = b2
−a2.
– Parabola : 4px = y2. Focus at (p, 0), directrix at x = −p. If the parabola is
of the
form 4py = x2, then the focus is at (0, p) and the directrix is y = −p.
– Hyperbola: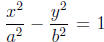
. Foci at (c, 0) and (−c, 0),
where c2 = a2 + b2. If the
hyperbola is instead 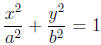, then the foci are at (0,
c) and (0,−c), where
c2 = a2 + b2 still. The asymptotes ar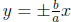e 
in
either case.
