ITERATIVE METHODS FOR SOLVING LINEAR EQUATIONS
ITERATIVE METHODS FOR SOLVING LINEAR EQUATIONS
There are other methods that can be used to solve a set of linear equations that
are based
on iteration. In these cases, an initial estimate of the parameters is estimated
and then the
equations are solved, yielding an updated version of the parameters. These new
values
are then inserted back into the equations and the process continues until the
desired
solution is reached . The two iterative methods discussed here are the Jacobi
method and
the Gauss-Seidel method.
Jacobi Iteration Method
Given a set of linear equations ,
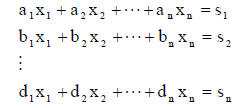
the problem is one of solving for x1, x2, …, xn. The right hand side of these
equations, si,
represents the solution. We begin by rearranging these equations in the form of
solving
for the unknown parameters one equation at a time. Thus,
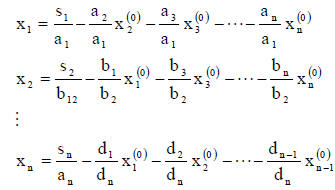
The superscript (0) indicates the initial estimate of the parameters. For the
first pass,
these parameters are given the value zero . The equations are then solved which
results in
an updated value of the parameters. These current estimates are then inserted
back into
the equations and a newer set of parameters is arrived at by solving these
equations. The
process continues until the solution converges.
As an example, take the following linear equations:
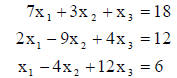
Rearrange these equations
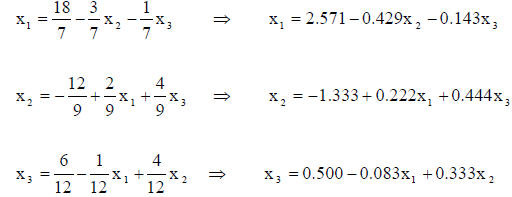
Use as the initial estimates: 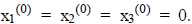 Insert these
estimates into these Insert these
estimates into these
equations yielding new estimates of the parameters.
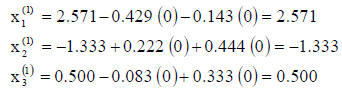
Insert these updated estimates back into original equation
again, yielding
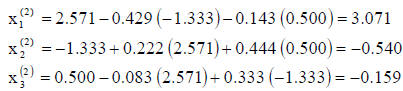
This process is continued until the desired results are
obtained. The following table
shows the solutions arrived at after each iteration. These results are from the
attached
Fortran program. The output shows x(i) that are the parameters xi. Also output
is the
change in the parameters , dx(i), between each iteration
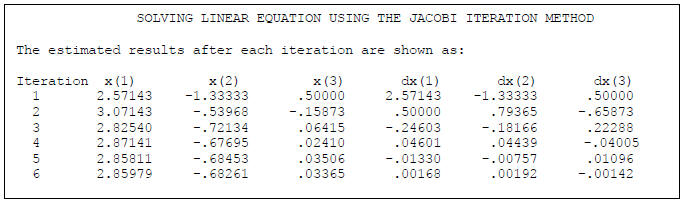
How good are these results? Lets take our equations and put them into an
augmented
matrix and solve using Gauss- Jordan elimination .
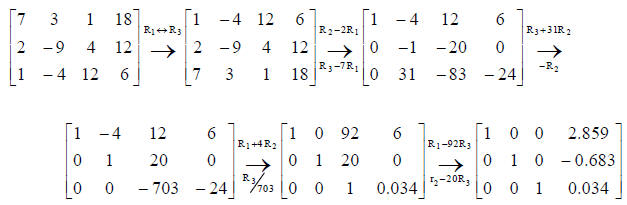
As one can see, the values using the Jacobi iterative
method are very close. Following is
a Fortran program that can be used to use the Jacobi iteration to solve a set of
equations.
The limitation now is that it is restricted to only a 3 x 3 matrix, due to
formatting
procedures currently used in the program.
c Program Jacobi
c Program to solve a linear equation using the Jacobi Iteration
c method
c
IMPLICIT none
REAL *8 coef(3,4), d, dx(3), x(3,4), xn(3), xnp(3)
INTEGER i, iter, iterate,j, no, nv
DATA iterate /0/
c
c The data are entered into the program using a data file called
c jacobi.dat. It has the following row values
c number of equations
c number of variables
c x(1) x(2) x(3) solution for the first equation
c x(1) x(2) x(3) solution for the second equation
c x(1) x(2) x(3) solution for the third equation
c
OPEN (4, file = 'jacobi.dat')
OPEN (6, file = 'results')
c
c no is the number of equations and nv is the number of variables
c
read(4,*) no
do 5 i=1,no
xn(i) = 0.d0
5 continue
read(4,*) nv
write(6,901)
c
c The coefficients for the variables are read in the matrix x with
c the solution to the equations being the last column
c
do 10 i=1,no
read(4,*)(x(i,j),j=1,no+1)
c
c d is the coefficient for the variable that is being solved for
c it forms the denominator to compute the real number for the
c remaining coefficients
c
d = x(i,i)
do 7 j=1,no+1
coef(i,j) = x(i,j)/d
7 end do
c
c Because the Jacobi method solves for the unknown variable with
c respect to the current estimates of the other variables, the
c coefficient for the variable is made to be zero for subsequent
c use in the loop to compute the adjusted estimates
c
coef(i,i) = 0.d0
write(6,900)(x(i,j),j=1,nv+1)
10 end do
write(6,902)
do 13 i=1,no
write(6,900)(coef(i,j),j=1,nv+1)
13 end do
write(6,903)
15 iter = 0
c
c iterate is just a counter to keep track of the number of iterations
c
iterate = iterate+1
c
c Solve for the estimate of the unknown parameters
c
do 20 i=1,no
xnp(i) = coef(i,nv+1)
do 18 j=1,nv
xnp(i) = xnp(i) - coef(i,j)*xn(j)
18 end do
20 end do
c
c dx is a vector showing the change in the estimate of the variable
c with respect to the estimated value used in the previous iteration
c
do 50 i=1,no
dx(i) = xnp(i) - xn(i)
c
c Test to see if the change is greater than the threshold
c If it is, then the variable iter is made equal to 1
c At the beginning of each loop, this value is made equal to 0
c If iter is 1 then this means to iterate again
c
if (dabs(dx(i)).gt.0.01d0) iter = 1
c
c Update the estimated parameter value
c
xn(i) = xnp(i)
50 continue
write(6,904)iterate,(xn(i),i=1,nv),(dx(i),i=1,nv)
if (iter.gt.0) go to 15
900 FORMAT(5x,4(f10.4,5x))
901 FORMAT(15x,'SOLVING LINEAR EQUATION USING THE JACOBI ITERATION MET
1HOD',//,'The coefficients to the equations with the solution at th
1e end are:',/)
902 FORMAT(//,'Rearranging the equations to solve for the unknown vari
1ables yields',/,5x,'the following coefficients: ',/)
903 FORMAT(//,'The estimated results after each iteration are shown as
1:'//,'Iteration',2x,'x(1)',9x,'x(2)',9x,'x(3)',7x,'dx(1)',7x,'dx(2
2)',7x,'dx(3)')
904 FORMAT(i3,4x,6(f10.5,2x))
stop
end
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
February 5th
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
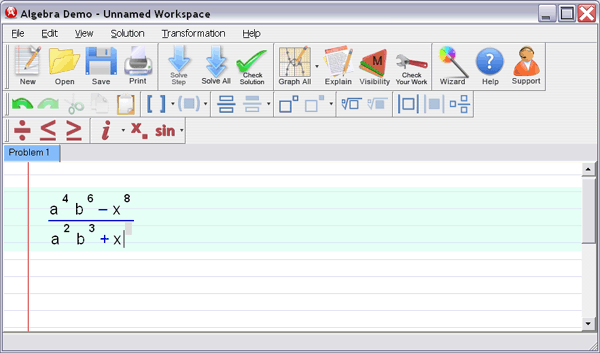
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
Step 2 :
Let Algebra Helper solve it:
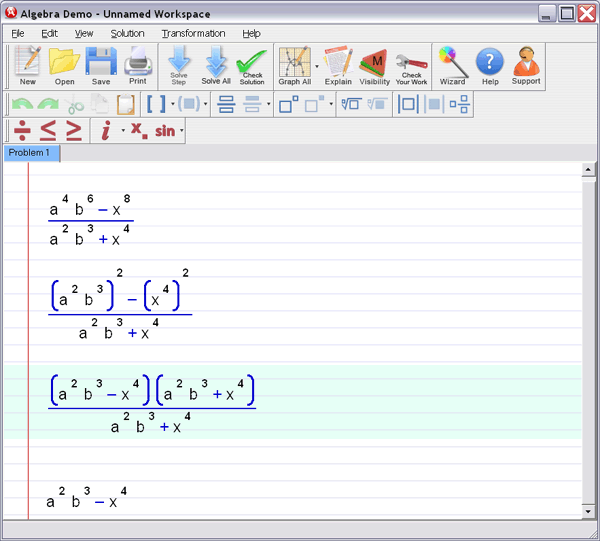
Step 3 : Ask for an explanation for the steps you don't understand:
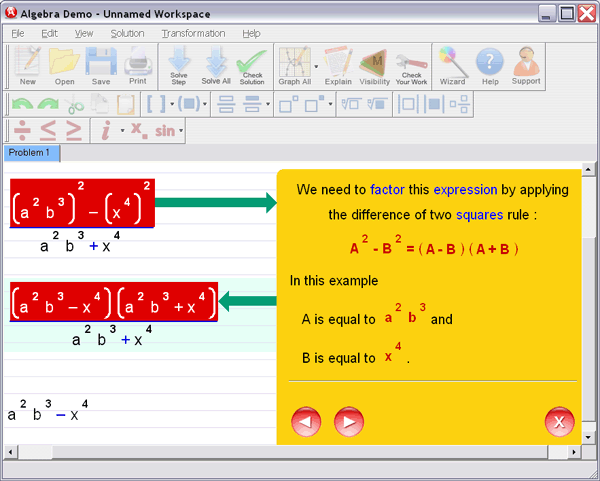
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



