An Important Application of Quadratic Functions :
Optimization
1. Factor out the coefficient of x2 from all terms.
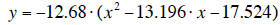
2. Add and subtract just the right amount to create a
perfect square
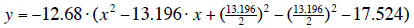
3. Factor the perfect square and combine the constants
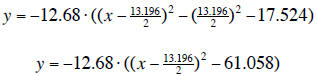
4. Distribute the factor that is out in front of the
equation
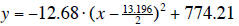
(e) The x- coordinate of the vertex is
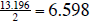, which marks the year when we
began to win the battle against perinatal HIV transmission in the United States.
This corresponds to the year 1991 or 1992. The y-coordinate of the vertex is
774.21, which means that during 1991 (or 1992) there were about 774 cases of
perinatal HIV transmission in the United States.
Example: Creating a Formula for a Quadratic Function from a Word Problem
 |
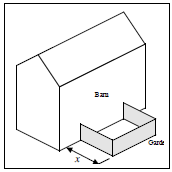A rectangular garden is constructed so that one
side of
the garden is against a barn. The remaining three sides
are enclosed using 100 feet of fence. (No fence is used
along the side of the barn.) The width of the garden is x.
(a) Express the area of the garden as a function of the
dimension x.
(b) Use the technique of completing the square to
convert your answer to Part (a) into vertex form. |
(c) What is the value of x that will give the biggest
(maximum area) garden? What is
the maximum area of the garden in square feet?
Solution
(a) The objective in this problem is to find a formula for the area that only
involves
the letter x and numbers.
When viewed from above, the barn and the garden will look something like the
diagram shown below. The width of the garden is x and the length of the garden
is L.
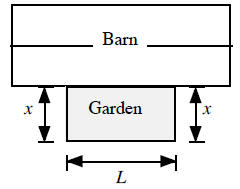
The area of the rectangular garden is equal to the width
(x) times the length (L).
Using algebra to express this as a formula gives:
Area = x · L.
The only problem with this formula is that it includes the letter L. The
objective
in this problem is to find a formula for the area that only involves the letter
x and
numbers. We will have to find a way to replace the L in the area formula.
The information that allows you to replace the L in the area formula is the fact
that there is only 100 feet of fencing material available for the project. This
means that the lengths of the three walls of the garden must add up to 100 feet.
Two of the walls are short (each having length x) and one of the walls is long
(having length L). Expressing this information using algebra:
2 · x + L =100.
The plan is to rearrange this equation to make L the subject. This will give a
formula for L that is expressed using x and numbers. This formula for L can then
be used to replace the unwanted L that appears in the area formula.
Rearranging to make L the subject of the equation:
L =100 - 2· x.
Using this formula for L to replace the unwanted L in the area formula:
Area = x · L = x · (100 - 2 · x) = -2 · x2 +100 · x .
This formula gives the area and only involves the letter x and numbers.
(b) Completing the square is a six- step process . The individual steps are
described
below and applied to the area formula from Part (a).
Step 1: Factor out the coefficient of x2
Area = -2 · x2 +100· x
Area = -2 · [x2 - 50 · x]
Step 2: Identify the new coefficient of x
Coefficient = −50
Half of coefficient = −25
Square of this = (−25)2 = 625
Step 3: Giveth and taketh away
Area = -2 · [x2 - 50 ·x]
Area = - 2· [x2 - 50 · x + 625 - 625]
Step 4: Factor the first three terms inside the square bracket
Area = -2· [x2 - 50 · x + 625 - 625]
Area = -2 · [(x - 25)2 - 625]
Step 5: Combine the remaining constants
Area = -2 · [(x - 25)2 - 625]
Step 6: Multiply out the number that is outside the square bracket
Area = -2 · (x - 25)2 +1250
(c) The x-coordinate of the vertex gives the value of x that will create the
largest
possible garden and the y-coordinate of the vertex gives the maximum possible
area of the garden. According to the vertex form found in Part (b), an x-value
of x
= 25 will lead to the largest possible garden and the maximum possible area will
be 1250 square feet.
Example
Figure 6 (see next page) shows an under- funded pre -school building and its
playground.
The under-funded pre-school can only afford to buy 400 feet of fencing materials
to
enclose their playground. To get the most out of their meager resources the
school
decides to build the fence around the school building, so that the walls of the
school
building will form part of the wall that encloses the playground.
(a) Use Figure 6, together with the fact that there is only 400 feet of fencing
material
available, to find an equation that combines x and y.
(b) How wide (y) and how long (x) show the pre-school make its playground in
order
to have the biggest possible playground.
Solution
(a) Figure 6 shows the fences that the school needs to put up, and the length of
each
section of fence. In total, this will be:
x + y + (x - 70) + (y - 50) = 2 · x + 2· y -120.
The total amount of fencing material that is available is 400 feet. This means
that
the equation obtained above must be equal to 400.
2 · x + 2· y -120 = 400.
Solving this equation to make y the subject:
2 · x + 2· y -120 = 400 
(Add 120 to both sides)
2 · x + 2· y = 520 
(Subtract 2x from both sides)
2 · y = 520 - 2· x 
( Divide both sides by 2)
y = 260 - x
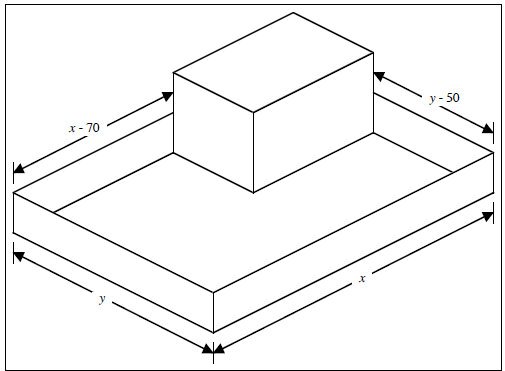
Figure 6.
(b) The playground can be sub-divided into three
rectangular parts, as shown in the
diagram given below.
One way to work out the total area is to find the area of
each of the three
rectangular portions of the playground, and then add these three formulas
together. Another way to work this out is to note that the total area is equal
to x·y
and that all but 3500 square feet consist of playground.
The area of the
playground is then:
A = x · y - 3500.
As this formula has to be expressed entirely in terms of x, you can use the
equation from Part (a) to replace the y in this formula.
A = x · (260 - x) - 3500 = -x2 + 260 · x - 3500.
To find the dimensions that give the largest possible playground, you can note
that the area formula is a “frowning” quadratic. The maximum area will be
located at the vertex of the area function. Converting the area formula to
vertex
form by the technique of completing the square gives:
A = -(x -130)2 +13400.
To maximize the area of the playground, x = 130 and y = 260 − 130 = 130.
