Reasons For Learning Fractions
Why are fractions important? Can you think of ways
fractions are used in
everyday life?
Money
Time
Cooking
Land
Looking At Common Misconceptions
Bring up some of the mistakes found during last
test.
1) Circles – A common misconception was to not divide the circle
into an
even amount of parts. (i.e. Is this circle cut up into thirds?)
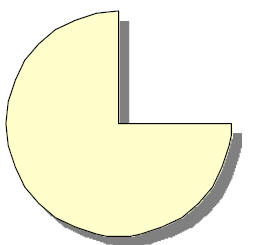
Have students discuss what is wrong with this
picture and then use overhead to
show them how to divide a circle into different fractions using the fraction
circle
manipulatives.
Have them use fraction circles to COMPARE 3/8 AND 5/16 and to COMPARE
2/3 AND 4/6.
2) Comparing Fractions
Some students wanted to say that 4/5 is larger than
7/10 because the difference
between the numerator and denominator is less than the difference of the second
fraction.
Ask why this method is not appropriate (can use the counterexample of
demonstrating
this does not work in the case of1/3 in comparison to 6/9). Show student s how
to
compare fractions by first reducing to lowest terms .
Examples will be to COMPARE 5/8 TO 12/16 and to COMPARE 6/9 TO 4/12.
3) Comparing unlike denominators
Students did not use the strategy of finding a
common denominator to compare
fractions. We will give the example of COMPARE 1/3 TO 1/4. We will show students
how to compare these two fractions by first finding the least common
denominator.
The next examples will be to COMPARE 2/3 TO 3/5 and to COMPARE 4/5 TO 6/7.
Talk about whether these fractions are equivalent and how to be able to tell
using LCD’s.
4) Comparing Decimals
While going over the test results, it was a common
mistake for students to ignore
the decimal point and then compare the resulting values. For example, students
placed
numbers in the following ascending order , .6, .8, .55, .125, .875 (They made the
error of
thinking 6 is smaller than 8 is smaller than 55 is smaller than 125 is smaller
than 875 and
not paying attention to place value.)
We will ask them to pay attention to place value and to COMPARE 0.60 TO
0.8
We will bring up concept of using a number line to order these numbers if they
do not
bring it up first. We will have them draw a number line and COMPARE 0.375 TO 0.5
and COMPARE 0.415 TO 0.25
5) Fractions to Decimals
We will build on the concept of decimals, place value and number line by
asking
them to COMPARE 3/4 TO 4/5 by first converting them both into decimals, then
comparing them by using a number line if necessary.
Next we will ask them to COMPARE 3/8 TO 3/7 and to COMPARE 2/5 TO 1/3
Issue Practice Problems
Talk about the different strategies used to compare problems
Play Fraction War Card Game
Break Students Up Into Groups Of Four
Talk about strategies used to determine who was right and who was wrong.
Closure
Highlight Four different Strategies to compare Fractions
Circles
Reducing fractions
Least common Multiple
Convert to Decimals and use a number line
Which method proved to be the most effective and why?
Why are fractions important?
Do you feel like after today , you have a better understanding of
fractions?
Why? How? Please explain?



