• Scaling and sums
• Transpose
• Rank-one updates
• Rotations
• Matrix vector products
• Matrix Matrix products
• BLAS
• “ Premature optimization is the root of all evil”
• First make the code produce the expected results
– Validation
– Then worry about performance
• Test individual components of the software separately
• Report and handle errors
• Validate input data
• BLAS – Basic Linear Algebra Subprograms
– Three levels:
• Level 1: Vector operations
• Level 2: Matrix-Vector operations
• Level 3: Matrix-Matrix operations
– Originally written in F77, the standard has evolved to contain
F77,F95,C,C++ libraries, each with their own version of the calling
program. The dcopy routine is used to copy two vectors and is given
by: f_dcopy for fortran users and c_dcopy for C users.
– BLAS 1 was originally designed for vector processors. BLAS 2 and 3
were designed for cache-based computers
• LINPACK (Linear Algebra Package )
– Linear equation and linear least squares solvers
– Based on level 1 routines in BLAS
Mathematical Libraries, cont’d
Mathematical Libraries, cont’d
• EISPACK (Eigenvalue Software Package)
– Computes eigenvalues and eigenvectors
• LAPACK (Linear Algebra Package)
– Originally designed to extend LINPACK and EISPACK on shared memory
vector and parallel processors
– Also implements highly- tuned system -dependend BLAS libraries, using BLAS
levels 2 and 3 wherever possible
• SCALAPACK (Scalable Linear Algebra Package)
– Designed to extend LAPACK routines to work on distributed memory
parallel machines
– Uses BLACS (Basic Linear Algebra Communications Subprograms) for
interprocessor communication
• BLAS,LINPACK,EISPACK,LAPACK,SCALAPACK can be downloaded
• PLAPACK (Parallel Linear Algebra Package)
– Parallel linear algebra routines using high levels of abstraction
– Allows implementation of advanced linear algebra routines
• FFTPACK (FFT Package)
– Complex and real fft routines (available from netlib.org)
• VSIPL (Vector/ Signal /Image Processing Library)
– Attempt to create an fft standard
Self-tuning Libraries
• PHIPAC (Portable High-performance ANSI C Linear Algebra
Subprograms)
– Run a performance tuner which stores information about particular
machine
to optimize BLAS routines
– Performance tuner can take days because it creates system-specific
versions of all BLAS routines
• ATLAS (Automatically Tuned Linear Algebra Software)
– System-specific information is placed into the design of one specific
subroutine which can be called by all BLAS routines.
• FFTW (Fastest Fourier Transform in the West)
– System-specific information created at runtime using a "planner", which
stores information used by "executor" functions during program execution
Commercial Libraries
• Hardware vendors sell highly-tuned versions of BLAS and
LAPACK
for their hardware
– Intel Math Kernel Library (MKL)
– HP MLIB (Mathematical Software Library)
– IBM ESSL (Engineering and Scientific Subroutine Library)
– SGI SCSL
– SUN Performance Library
• Other libraries developed independently of BLAS,
specifically for
relevant hardware.
– Visual Numerics' IMSL (Mathematical and Statistical Library)
– Numerical Algorithms Groups' Numerical Libraries
BLAS Structure
Names are cryptic, follow a pattern
Prefix Matrix Type Name
• Example: DGEMM: double precision
matrix multiplication of a general full matrix
• First versions written in Fortran 77
– 1-based indexing
– Call by reference
– No dynamic memory allocation
BLAS, cont’d
| Prefix |
Fortran type |
| S |
Real |
| D |
Double precision |
| C |
Complex |
| Z |
Double precision complex |
| Type code |
Matrix type |
| GE |
General full |
| SY |
Symmetric |
| HE |
Hermitian |
| TR |
Triangular |
| GB |
General banded |
| SB |
Symmetric banded |

Simple Vector Operations (BLAS level 1)
• Setting to zero or a specified constant
• bzero = set elements to zero
for(i=0;i<N;i++)
y[i]=0;
• memset = set elements to a specified constant
for(i=0;i<N;i++)
y[i]=value;
• Vector copy
• c_dcopy=Double precision vector copy y=x
for(i=0;i<N;i++)
y[i]=x[i];
Scalar-Vector accumulation
• daxpy=Double precision y=a*x+y
for(i=0;i<N;i++)
y[i]+=a*x[i];
• daxpby=Double precision
y=alpha*x+beta*y
for(i=0;i<N;i++)
y[i]=alpha*x[i]+beta*y[i];
• Compiler will unroll these loops
Dot Product: BLAS ddot
No unrolling:
for(i=0;i<N;i++)
ddot+=x[i]*y[i];
Two-way loop unrolling:
for(i=0;i<nend;i+=2) {
ddot1+=x[i]*y[i];
ddot2+=x[i+1]*y[i+1];
}
• Effect of loop unrolling with N=1024 (8 kb), in MFlops
gcc –O0:
0: 235.90
2: 538.41 (2.28x)
4: 941.68 (3.99x)
6: 1024.97 (4.34x)
8: 1071.04 (4.54x)
10: 1053.29 (4.46x)
12: 1063.94 (4.51x)
14: 1061.28 (4.50x)
gcc –O2:
0: 223.60
2: 553.34 (2.47x)
4: 1092.23 (4.88x)
6: 1449.38 (6.48x)
8: 1548.78 (6.93x)
10: 1594.80 (7.13x)
12: 1572.16 (7.03x)
14: 1529.57 (6.84x)
• Loop unrolling reduces
overhead and allows for
pipelining
• Too much unrolling leads to
register spilling
Some BLAS Level 1 Routines
| Routine |
Operation |
Memory
ops per
iteration |
Floating point
ops per
iteration |
F: M ratio |
| dcopy |
yi=xi |
2 |
0 |
0 |
| daxpy |
yi=yi+a*xi |
3 |
2 |
0.67 |
| daxpby |
yi=β*yi+a*xi |
3 |
3 |
1.00 |
| ddot |
ddot=ddot+xi*yi |
2 |
2 |
1.00 |
BLAS Level 2 routines
• Level 2 routines consist of 2 loops and include matrix
copy, matrix transpose, and matrix-vector routines.
• Matrix copy: dge_copy
Performs well because of unit stride on inner-most loop:
for(i=0;i<N;i++)
for(j=0;j<N;j++)
b[i][j]=a[i][j];
The transpose case is not as straightforward:
for(i=0;i<N;i++)
for(j=0;j<N;j++)
b[i][j]=a[j][i];
gcc –O2 (1024 X 1024 int)
Copy: 707.31 Mb/s
Transpose: 54.59 Mb/s
Transpose with 1-d blocking
1-d blocks (a and b ints):
int en = bsize*(n/bsize);
for(jj=0;jj<en;jj+=bsize)
for(i=0;i<n;i++)
for(j=jj;j<jj+bsize;jj++)
b[i][j]=a[j][i];
• After i=0 inner loop (assuming 32-byte cache blocks):
– 8*bsize elements of a in L1 cache (a[0:bsize-1][0:7])
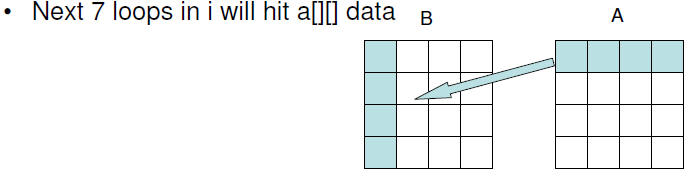
Transpose with 2-d blocking
2-d blocks (a and b ints):
int en = bsize*(n/bsize);
for(ii=0;ii<en;ii+=bsize)
for(jj=0;jj<en;jj+=bsize)
for(i=ii;i<ii+bsize;i++)
for(j=jj;j<jj+bsize;j++)
b[i][j]=a[j][i];

Effect of Blocking on Transpose
Performance (1024 x 1024 int)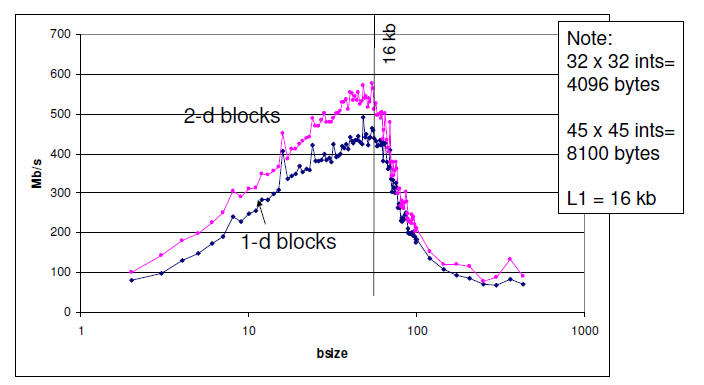
Peak throughput occurs when bsize=45
(when two 45x45 matrices fit into L1 cache!)
In-place Transpose: dge_trans
• Previous examples involved a copy and transpose
– This is termed out -of-place matrix transpose
• Consider the in-place matrix transpose (method 1):
for(i=0;i<n-1;i++)
for(j=i+1;j<n;j++) {
temp = a[i][j];
a[i][j] = a[j][i];
a[j][i] = temp;
}
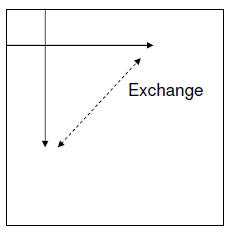
Move along a column and swap elements.
suffers from possible cache thrashing when n is a power of 2 since a[i*n+j]
and a[j*n+i] can map to same cache location
In-place Transpose: Method 2
for(i=0;i<n;i++)
for(j=i;j<n;j++) {
temp = a[j-i][j];
a[j-i][j] = a[j][j-i];
a[j][j-i] = temp;
}
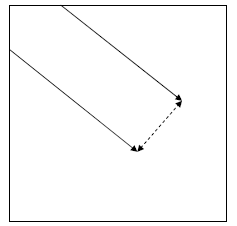
Move along diagonals and swap elements.
• This method is less likely to incur cache thrashing
when n is a power of 2 since stride is n+1 in j-loop:
• a[j-i][j]=a[(j-i)*n+j]=a[(n+1)*j – i*n]
• The BLAS routines employ blocking for in-place
transpose
• BLAS level 1: single-loop
– Set to zero (bzero), set to a constant (memset), copy vectors
(dcopy), inner-product (ddot), ax+y (daxpy), ax+by (daxpby)
• BLAS level 2: double-loop
– matrix copy (dge_copy), matrix transpose (deg_trans), outerproduct
(dger), matrix-vector product (dgemv)
• BLAS level 3: triple-loop
– matrix-matrix product (dgemm): optimized in-cache matrix solver .
For use with dge_copy to create a blocked matrix-matrix
multiply.
LAPACK
• Builds on BLAS for more linear algebra
• Linear Systems
– LU, Cholesky
• Least Squares
– QR
• Eigenproblems
• Singular Value Decomposition (SVD)
Dense Linear Algebra
• Matrix Decompositions
– Linear systems
• Symmetric,Nonsymmetric
– Least squares
• QR, SVD
• Eigenvalues
– Rayleigh iteration
– QR algorithm
• Standard libraries
– Linpack, Lapack, Atlas, PetSC, MKL



