Completeness Axioms - Real Numbers

The Real Numbers R are defined by Completing the rational numbers.
This means we add limits of sequences of rational numbers to the field . We
should then check that all the field axioms hold and that the ordering properties
persist. The Real Numbers are characterized by the properties of
Complete Ordered Fields. In these notes we give definitions of these terms.

Definition 0.1 A sequence of real numbers is an assignment of the set of
counting numbers of a set 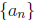, 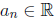of real numbers, .

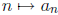Definition 0.2 A sequence 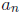of real numbers has a limit a if, for every
positive number ε > 0, there is an integer N = N(ε) such that
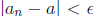
for all 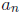with n > N.

Example 1: The sequence 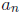= 1/n has limit 0 since we can take N =
[1/ε] + 1. This says

1/n < 1/(1/[epsilon] + 1) < ε, for all n > N

Example 2: The sequence 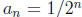has limit 0 since we can take N >
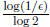. This says

1/2ⁿ < ε, for all n > N

Here is a list of equivalent statements . We can choose any one of them
as an axiom for completeness. Choosing one, we can prove that all the other
properties hold:

1. A field is complete if every infinite continued fraction has a limit .
(Nested Intervals) If 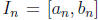is an infinite sequence of closed intervals
with 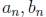in the field such that 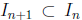In then the field is
complete if the infinite intersection of the intervals is non-empty, that
is, .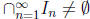

2. (Dedekind Cuts) A subset of a field is called a cut if: 1) It is non-empty,
but is not the whole set of rationals 20 every rational number of the
set is smaller than every rational number not in the set, 3) it does no
contain a number that is greater than any other number of the set. A
field is complete if it contains cuts.

3. (Greatest lower bound or Least upper bound) A lower bound for a set
is a number less than every number in the set, that is, if B ≤ x for all
x in the set, B is a lower bound. G is a greatest lower bound for the
set if it is a lower bound and every lower bound B satisfies B ≤ G.
Least upper bounds are defined similarly. For a complete field every
set that has a lower bound (upper bound) has a greatest lower bound
(least upper bound). The bound may or may not be in the set.

4. A field is complete if every bounded monotonic sequence has a limit.

5. If 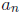is a sequence with the following property: given ε > 0 there exists
an N = N(ε) such that for all m, n > N we have 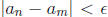then
the sequence is called a Cauchy Sequence. A field is complete if every
Cauchy sequence has a limit.

Example 3: Let 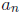be the finite decimal whose n entries are the first n digits
of the infinite decimal for 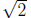. Then 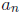is monotonic increasing, bounded
by 2, and has limit 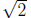(the least upper bound). Example 4: Consider the
sequence 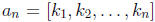of continued fractions. Let 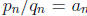. Then
it is not hard to show that the intervals 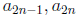are nested. The diameters
of the intervals goes to zero so the infinite continued fraction is the unique
point in the intersection. One way to prove this uses the cutting sequence
technique. 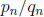and 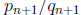have cutting sequences that agree until the
last set of L's (or R's). If the sequence ends in L's it is to the left of the
number and if it ends in R's it is to the right. Note that 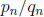and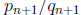
must be neighbors.

Example 5: Consider the sequence 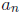= [1, 1, ... , 1] where there are n 1's
in the continued fraction. Let 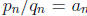. It is easy to check that
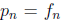
and 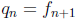where 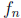is the n^th Fibonacci number. Then the sequence
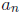
is a Cauchy sequence. The limit is .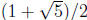

For real numbers we can talk about continuous functions and define
derivatives. Consider the polynomials x² - r = 0 for r > 0. We can graph
them. Because of the completeness of the reals, the graph is continuous and
must cross the x axis in two places. These are the roots of the equation . For
all odd degree polynomials we can see that they must cross the x axis in at
least one place so they have at least one real root. Note though that not all
polynomials have real roots. For example x² + 1 = 0.

Complex Numbers

If we want to solve for roots of all algebraic equations , f(x) = 0, we need
to introduce complex numbers. We look at pairs of real numbers (x, y) and
define the following operations for them :



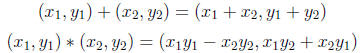
Taking the additive identity as (0, 0) and the multiplicative identity as (1, 0)
it is possible to check that the pairs of numbers with this operation define
a field. Note that it is NOT an ordered field! We set z = (x, y). We can
plot the complex numbers as points in a plane using the first and second
coordinate as the horizontal and vertical coordinates. Using the standard
distance in the plane we can define the distance between two points



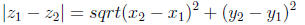
Using this distance we can define Cauchy sequences. One can prove that
all Cauchy sequences have limits using the fact that the coordinates are real
numbers. It follows that the complex numbers are a COMPLETE field.

The distance from a point z to the origin (additive identity), (0, 0) is
lzl = sqrtx² + y². We can specify a point z by its distance from the origin
and the angle a line joining the point to the origin makes with the horizontal
axis. Call this angle θ.

Exercise: Show that if r = lzl and θ is the angle defined above,

z = (x, y) = (r cos θ, r sin θ)

Addition of complex numbers can be thought of as addition of vectors. To
find the sum 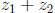, draw the line from the origin to 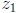, then translate the
line from the origin to 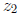so that it starts at the end of the first line. The final
endpoint is the sum. Multiplication of complex numbers also has a geometric
interpretation: if 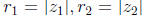and the corresponding angles are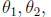
then 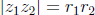and the angle that 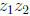makes with the horizontal is
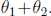
This leads us to define

e^iθ = (cos θ, sin θ)

to describe points on the unit circle . It is clear that le^iθl = 1 since cos² θ +
sin² θ = 1. We see from the multiplication law that we have DeMoivre’s
theorem:

e^inθ = (cos nθ, sin nθ)

Note that there is another notation that we often use:

(x, y) = x + iy

We think of (0, 1) = i as the imaginary number that solves x² +1 = 0. That
is, i² = -1. We have the following interesting formula: .
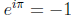