Key Idea 1
Mathematical Reasoning
Assessment Examples
5G.
As one of its admissions criteria, a college requires an SAT math score that is
among the top 70% (69.1%) of all scores.
The mean score on the math portion of the SAT is 500 and the standard deviation
is 100. What is the minimum acceptable
score? Justify your answer by drawing a sketch of the normal distribution and
shading the region representing
acceptable scores. [Also 6G.]
5H.
Use your knowledge of the area of squares and triangles to derive the
Pythagorean Theorem.
5I.
A business owner pays each of his employees $50,000 per year. His salary is
$150,000 per year. He wants to place an ad
in the newspaper for more help. What would be the problem with only mentioning
the mean with regard to salary?
What measures of central tendency are more accurate when discussing salary?
Would it be helpful to mention dispersion?
Why? Support your answers with calculations.
5J.
Record, in seconds, the time for each student to run a 100 meter dash. Also
record their height in inches. Sketch a scatter
plot of the data (Use a minimum of 10 students.).
• Can any conclusions be made concerning height and speed?
• Using a calculator, find the equation of the best fit line.
• Does this equation support your conclusions?
• Make predictions for other students based on their height.
• Discuss the accuracy of these predictions.
6A.
The following ads for truck rentals appear in the paper.
| Easy Rent-A-Truck |
Fast Rent-A-Truck |
| $30 per day plus $2 per mile |
$60 per day plus $1 per mile |
A. You plan to rent a truck for one day. From which company would you rent? Why?
Suppport your answer with a discussion
of the factors you need to take into consideration. Use both equations and
graphs to help illustrate your
solution. Substitute specific values to check your results.
B. Determine under what conditions, considering both days and milage, the
expense of renting a truck from Fast Rent-
A-Truck would be less expensive than renting from Easy Rent-A-Truck.
6B.
A rich philanthropist, who loved mathematics, agreed to sponsor an 18-hole golf
tournament at the local country club.
In order to enter, a contestant had to pay 2 cents and select either a linear ,
quadratic , or exponential formula to calculate
how many CENTS he/she would receive for a winning hole. In each of the following
formulas, x represents the number
of the winning hole. linear, y = 2x; quadratic, y = x2, exponential, y = 2x. Why
bother entering if the payoff is in pennies?
Use your graphing calculator to investigate. Describe numerically how the
amounts change from one hole to the
next for each method. Which method would you select on your entry form and why?
6C.
The principal of the local high school was willing to participate in the school
fair dunking booth in which students who
paid $1 could push a button that operated a light over the booth which was
programmed to flash either red or green. If
the light flashed green, the principal would fall into the water. If it flashed
red, he would not. He was told that the light
was set to flash either red or green randomly with a 50% chance of turning
green. As it turned out, the principal seemed
to be dunked more than 50% of the time. In the first 20 pushes of the button, he
was dunked 15 times . He was getting
suspicious that probability had been misrepresented to him. Based on the results
so far, do you think the principal has
justification for being suspicious? What is your reasoning? If you do not think
the principal is justified in his suspicions,
how many occurrences of 75% dunks would it take to convince you that the light
was not set at 50% green? If you think
the principal is justified in being suspicious, what are the smallest
occurrences of 75% that would be required to convince
you? [Also Performance Indicators 6C., 6D., and 6E.]
6D.
If each problem can be regarded as a Bernoulli experiment, state the values of
n , p, q, and r, and give the answer in symbolic
form. If the problem cannot be regarded as a Bernoulli experiment, explain why.
Four balls are drawn with
replacement from an urn containing 4 red balls and 2 white balls.
What is the probability of drawing exactly 2 red balls?
Four balls are drawn without replacement from an urn containing 4 red balls and
2 white balls.
What is the probability of drawing exactly 2 red balls? [Also Performance
Indicator 6F.]
6E
Given x = {10, 20, 30, 40, 50} and y = {11.0, 12.1, 13.0, 13.9, 15.1} where x is
measured in lbs. force and y measures the
length of a spring in inches.
• Find the equation which best fits the data.
• Determine the load when y = 17 inches and determine the length of the spring
when x = 62 lbs.
6F.
In her algebra class , Ms. Goodheart predicts 8 of her 26 students will earn a
score of 90 or above on a particular exam
with a normal distribution. After taking the exam, the mean score was 84 with a
standard deviation of 6. Was her prediction
accurate? What should she have predicted to be more precise?
6G.
The boiling point of water is a function of altitude. The table shows the
boiling points at different altitudes.
Location
|
Altitude
h meters |
Boiling point of
water, t°C |
| Halifax, NS |
0 |
100 |
| Banff, Alberta |
1383 |
95 |
| Quito, Ecuador |
2850 |
90 |
| Mt. Logan |
5951 |
80 |
- Graph the relation between the altitude and the boiling point.
- Use the graph to estimate the boiling point of water at:
a) Lhasa, Tibet, altitude 3680m
b) the summit of the Earth ’s highest mountain, Mt. Everest, 8848m.
7A.
f(x) = x3 + 5
A. Does f(x) have an inverse?
B. If so, find the inverse and decide if it is a function
7B.
A projector throws an image on a screen. To determine how the width of the image
is related to the distance of the
screen from the projector, the following measurements were made.
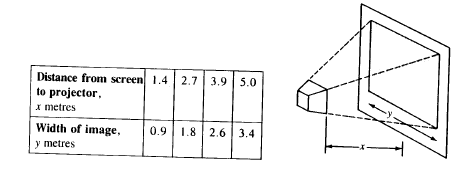
Graph the data and find the equation relating x and y.
Find the width of the image when the projector is 3.0 m from the screen.
Find the distance from the projector to the screen when the image is 3.0 m wide.
What is the domain of the relation?
7C.
A printer agrees to print a brochure for a sum of $300 plus 15 cents for each
copy. Express the cost as a function of the
number of copies.



