Elementary Matrix Operations and Elementary Matrices
Left- Multiplication Transformations
Theorem
Let A and B be n × m matrices. Then
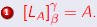
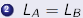 if and only if A = B. if and only if A = B.
 and and
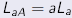 for all a ∈ F. for all a ∈ F.
 If If 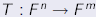 is linear , then there
exists a unique m × n is linear , then there
exists a unique m × n
matrix C such that 
 |
Change of Coordinates for Left -Multiplication
Transformations
Theorem
Let A be an n × n matrix and let γ be an ordered basis for Fn.
Then
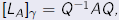 where Q is the n × n matrix whose jth where Q is the n × n matrix whose jth
column is the jth vector of γ. |
Definition
Let A be an m × n matrix. Any one of the following three
operations on the rows [columns] of A is called an elementary row
[column] operation :
 interchanging any two rows
[columns] of A. (type 1) interchanging any two rows
[columns] of A. (type 1)
 multiplying any row [column]
of A by a nonzero scalar. (type 2) multiplying any row [column]
of A by a nonzero scalar. (type 2)
 adding any scalar multiple of a row [column] of A to another
adding any scalar multiple of a row [column] of A to another
row [column]. (type 3) |
Elementary Matrices Operations
Definition
 An n × n elementary matrix is a matrix obtained by
An n × n elementary matrix is a matrix obtained by
performing an elementary operation on I n.
 The elementary matrix is said to be of type 1, 2, or 3
The elementary matrix is said to be of type 1, 2, or 3
according to whether the elementary operation performed on
In is a type 1, 2, or 3 operation, respectively. |
Multiplying with an Elementary Matrix
Theorem
Let 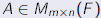 , and suppose that B is obtained
from A by , and suppose that B is obtained
from A by
performing an elementary row operation . Then there exists an
m × m elementary matrix such that B = EA. In fact, E is obtained
from Im by performing the same row operation as that which
was
performed on A to obtain B.
Conversely, if E is an elementary m × m matrix, then EA is the
matrix obtained from A by performing the same elementary row
operation which produces E from Im. |
Every Elementary Matrix is Invertible
Theorem
Elementary matrices are invertible, and the inverse of an elementary
matrix is an elementary matrix of the same type. |
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
January 22nd
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
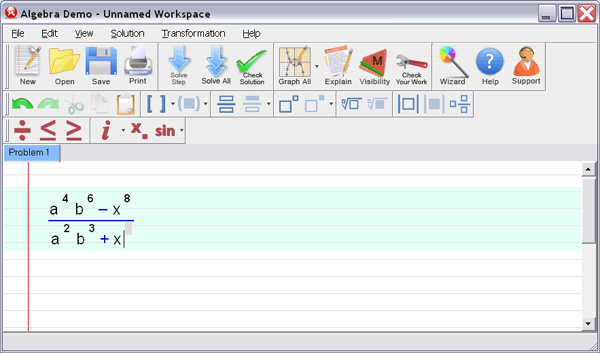
Step 2 :
Let Algebra Helper solve it:
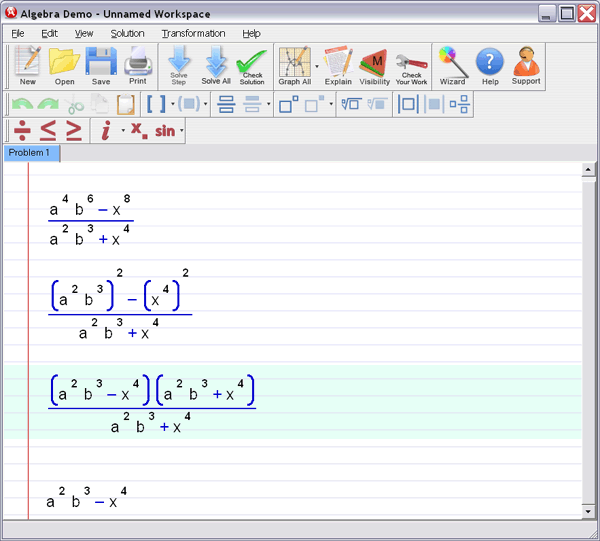
Step 3 : Ask for an explanation for the steps you don't understand:
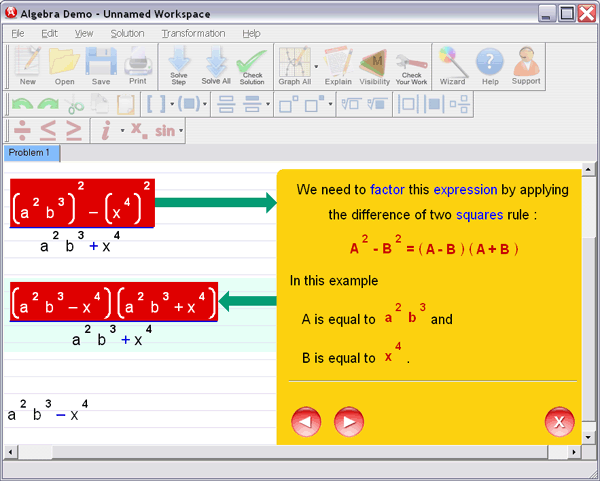
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |