Solutions to Math496 Homework

1. Show that 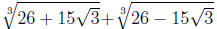is a rational number. Hint: Find
rational numbers a , b, c, and d such that 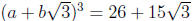and

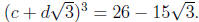
Following the hint, we see that if 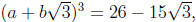then

a³ + 9ab² = 26 and
3a²b + 3b³ = 15:

Checking to see that a = 2, b = 1 is a solution to this equation , we
then have that 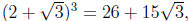and hence

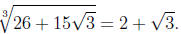
Similarly, one checks that 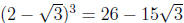so that

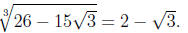
Consequently, 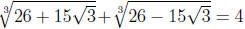which is a rational number.

2. Find a polynomial with rational coefficients that 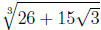is a root
of. For this problem, there are a variety of answers. By the previous
problem, 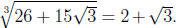If we write 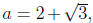then we know
that 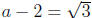so that (a - 2)² = 3. Thus

a² - 4a + 4 = 3;

yielding that a² - 4a+1 = 0. Thus a is a root of x² - 4x+1. To check
this answer, we can use the quadratic formula to see that indeed, a is
one of the roots of this equation .

A second solution comes by writing 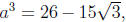so that we obtain
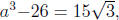and squaring both sides we obtain that a⁶ - 52a³+676 =
675. Consequently, a⁶ - 52a³ + 1 = 0, and a is a root of x⁶ - 52x³ + 1.

Is there a relationship between our two answers? Of course, there
should be since we know from abstract algebra that the minimum polynomial
for a should divide every other polynomial that has a as a root.
Doing long division, we see that

x⁶ - 52x³ + 1 = (x² - 4x + 1)(x⁴ + 4x³ + 15x² + 4x + 1):

Other students came up with a solution by looking at
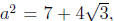
and subtracting off 7 to get 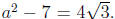Squaring yields that a⁴ -
14a²+49 = 48, so that a⁴ - 14a²+1 = 0, and a is a root of x⁴ -14x²+1.
Again, we can factor this polynomial as

x⁴ - 14x² + 1 = (x² - 4x + 1)(x² + 4x + 1):

3. Solve with radicals by hand (showing your work) the equation

x³ + 6x = 12:

One can do this by simply plugging in for p and q in our formulas,
but this is not how you do it in practice unless you have the formulas
memorized or easily available. For me, I simply remember the picture
of the cube that we had , so that I know that I want to set up u and v,
where (u - v)³ +3uv(u - v) = u³ - v³. Thinking of x = u - v, we want
6 = 3uv and 12 = u³ - v³. From here, we solve the first equation for v to
get that v = 2/u, so that the second equation becomes 12 = u³ - (2/u)³.
Multiplying through by u³, we obtain 12u³ = u⁶ - 8, so that we want
u to satisfy u⁶ - 12u³ - 8 = 0. This is a quadratic in u³, so that the
quadratic formula gives us

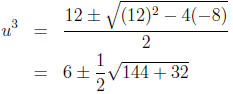
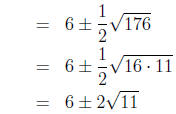
Thus, we can set 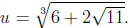We can now solve for v³ by noting
that 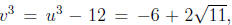so that 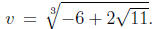Since
x = u - v, we have

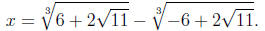
Checking this on our calculator suggests that it is correct.

I did the problem this way, to show how one usually solves cubic equations
in practice. That is, rather than memorize a complicated formula,
it pays to remember the main idea (the picture of the cube), and then
solve the problem algorithmically. You can do something very similar
with the quadratic formula, where you remember only the picture of
the square, and then ll in the numbers as you go along. In particular,
you should note how I didn't exactly follow the steps that we did in
class. Rather than holding onto the terms 6/2 and p/3, I was able to
reduce immediately and use the reduced terms in my formulation.

Compare this to solving a quadratic equation where a = 1, and b and
c are both even. The quadratic formula requires you to cancel out a 2
along the way, but if you actually solve the equation by completing the
square, or using the geometric algorithm with the square, the 2 that
needs to be cancelled out of the 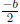term and the square root has been
cleaned up.

4. Solve with radicals by hand (showing your work) the equation

x³ + 3x² + 15x + 3 = 0:

We begin by noting that we wish to eliminate the 3x² term. To do so,
we let x = y - 1. Then plugging in y - 1 for x we obtain

y³ - 3y² + 3y - 1 + 3(y² - 2y + 1) + 15(y - 1) + 3 = 0;

which simplifies to

y³ + 12y - 10 = 0:

Since we just did the other process by hand, I will work on this one
by the formula. Putting the above equation for y in our \standard
form," we obtain y³+12y = 10. Thus p = 12 and q = 10, yielding that
p/3 = 4, and q/2 = 5. Using the formula for the standard cubic that
we obtained, we have

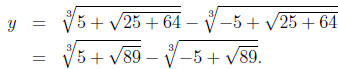
As x = y - 1, we have that

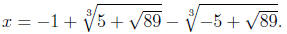
5. It is unknown whether eπ and e + π are transcendental or not. Curiously,
it is known that at least one of them must be transcendental.
Use the following outline to prove this:

(a) Show that either e+π or e - π is transcendental. (You are allowed
to use that e and π are transcendental, and that the algebraic
numbers form a eld.)

(b) Calculate (e +π )² - 4eπ and factor.

(c) Using that the algebraic numbers are closed under square roots,
show that if both e+π and eπ are algebraic then e - π would also
be algebraic.

(d) Using the first part, show that either e+π or eπ is transcendental.

I will write this proof in one short proof, rather than do the step-by-step
outline.

Let us begin by assuming that e+π is algebraic (otherwise there would
be nothing to prove). If e - π were also algebraic, then e + π +(e - π ) =
2π would also be algebraic since the algebraic numbers are closed under
addition. As the algebraic numbers are also closed under multiplication,
this would imply that 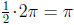was algebraic, which is a contradiction.
Consequently, e - π must be transcendental in this case.

Since (e+pi)² - 4eπ = e² - 2eπ + π² = (e - π)², if both e+pi and 4eπ
were algebraic, then (e - π)² would also have to be algebraic. However,
the algebraic numbers are closed under square roots since if α is a root
of p(x), then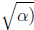  is a root of p(x²) which is a polynomial if p(x) is.
Consequently, if both e+π and eπ are algebraic, then e - π would have
to be algebraic. This, however, is a contradiction to the first paragraph,
so if e+π is algebraic, then it must be the case that eπ is not algebraic
and is thus transcendental.

6. Discuss the difference between transcendental and algebraic numbers
and how this affects a student's ability to understand each. How might
this influence your teaching about π and e?

An algebraic number is a number that is the root of a polynomial with
integer coefficient. A real number is transcendental if it is not algebraic.
Thus, a transcendental number is not the root of any polynomial with
integer coefficients. In addition to making these concepts opposites,
this also means that a transcendental number is defined negatively , in
that it is only be defined by properties that it doesn't satisfy rather
than by properties that it does satisfy. When students encounter algebraic
numbers, they have a pretty solid foundation for working with
it. Graphing the polynomial by hand or on a calculator, they can zero
in on where the roots of the polynomial lie, and pretty quickly, they
can assign the number to a place on the number line. They also have
one of the main properties that defines this number at their fingertips,
namely that it is a root of the polynomial. For example,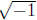 despite
being a complex number , is relatively easy for students to deal with
algebraically, even if they have some concerns over what it represents.
In contrast to algebraic numbers, transcendental numbers must be de-
fined by properties that the students are less likely to be familiar with.
For example, transcendental number that students might see (without
ever hearing that it is transcendental) is 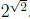This number is much
harder to zero in on . Certainly, the student's calculator can calculate
an approximation for it, but for the most part, the decimal approximation
of 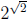is how the students will define the number internally,
as opposed to the number 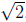  which the students will internally define
as a number that squares to 2.

Thus, when introducing students to transcendental numbers, the teacher
has two basic alternatives. The first is to introduce the number and
try and have the students think about it by its decimal approximation,
and the second is to give the students some other defining property. As
I believe that students are far too likely to treat decimal expressions as
the definition of a number (leading to difficulties with ,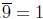), it seems
to me that the teacher should choose the second alternative whenever
possible.

For π this isn't too bad. Most students will be introduced to π early on
as the special number that helps us find the area of a circle . They also
will hear of it as being defined as the ratio of the circumference to the
diameter of a circle. Consequently, when teaching π, you can emphasize
the property, and then come back to the idea of approximations.

The number e on the other hand is a problem this way. While many
classical texts introduce e via instantaneously compounding interest,
the very next statement is that e is the number that is approximately
2:71828182845945…This, of course, leads the students to treat e
as its decimal approximation. The main problem with this is that e
becomes mostly unmotivated to the students, and thus it becomes a
number that they treat as one of those silly things that math teachers
force us to learn. So, what properties could we use to introduce e?
We want them to somehow be natural properties for students to think
about. One high school math textbook uses two such properties, that
e is the number so that the function e^x has slope 1 at x = 0, and that
e is the number so that the area under the graph of 1/x between 1 and e
is equal to 1. From the advanced viewpoint, we recognize that both of
these definitions require some fundamental understanding of calculus.
However, neither actually requires calculus. The first requires that
the students understand the idea of slopes of tangent lines, which is
really the idea of rate of change. The second requires that the students
understand the idea of area. The trick is that when we divide algebra
and geometry, defining a number by area makes some students feel
uneasy. The number π is typically introduced when students are used
to thinking about many areas of mathematics at once, so it doesn't run
into this problem, while the number e does.