Integration by parts, and mixing methods of integration

Comments on Written Assignment 2: Integration by parts, and mixing methods of integration

A note about comments on written assignments. When it comes to writing up solu-
tions/comments for writing-intensive assignments, unlike quizzes , I try to take the Sample Answers
mostly from answers that were actually submitted by students (quoted anonymously, of course).
These “notable quotes” are great models for others to use to get a sense of good student writing
on mathematics .

The “notable quote” Sample Answers are shown in quotation marks. Unquoted material in the
Answers and Comment sections represents my own remarks.

Motivation: We have seen that there is (alas) no Product Rule for integration that matches the
Product Rule for differentiation. Also, it is generally not true that the integral of the product of
two functions is the product of their integrals:

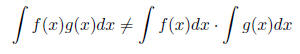
However, the techniques called u- substitution and Integration by Parts (IBP) allow us to integrate
certain particular kinds of products. We will see in this assignment how we can combine these rules
to expand the variety of functions that we’re able to integrate.

The u-substitution rule

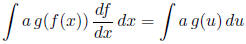
where 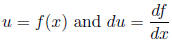, and a is a constant.

The Integration by Parts rule

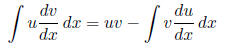
1. (10 points) Explain, in your own words, how you can tell when a product of functions in an
integral can be integrated with a u-substitution, and when it should be integrated with IBP.

Sample Answer: “It is fairly simple to determine whether to use u-substitution or IBP (Integra-
tion by Parts) to solve for the integral of a product of functions. u-substitution is helpful when
the one part of the product is a composition of functions (i.e., f(g(x))) and the other part of the
product is the derivative of the inside function (i.e., g′(x)). However, when the two functions in
the product have nothing to do with each other, that is, there is no composition of functions and
neither part is the derivative of the inside function of the other part, IBP should be used.”

Comment: It was crucial to mention that for u-substitution, the product in the integrand has
to contain a composition of functions or one function inside another, multiplied by the derivative
of the inside function. (A special case of that is when a function is composed with the identity
function—that is, you don’t do anything to it—and then multiplied by its own derivative. But
it’s important to note that u-substitution works on composed functions too, as long as they’re
multiplied by the derivative of the inside one.)

And it wasn’t really enough just to state the “trial-and-error” approach, as in “try u-sub first and
if it doesn’t work, do IBP”. That’s a good rule of thumb , but we want to know how to do the
integration more efficiently by understanding the key things about the integrand.

Grading: Partial credit for explanations that were partly accurate but not complete.

A combination of IBP and u-substitution can sometimes be used to compute integrals of functions
we can’t integrate in other ways. For example, we don’t have a standard antiderivative formula for
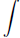arcsin(x) dx, but we can calculate one as follows:

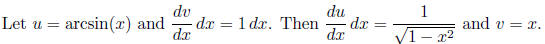The IBP rule gives us

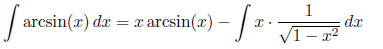
And this new integral can be computed using the u-substitution u = 1 − x^2:

Putting the two parts together, we get

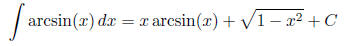
2. (20 points) Now use a similar approach to find antiderivative formulas for the following functions:

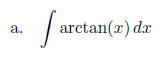
Sample Answer: “First, IBP can be used. Let u = arctan(x) and
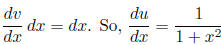
and v = x. Using the IBP rule we get: 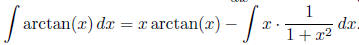. The second
part of the equation can be computed with u-substitution. We let 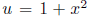. So du = 2x dx,
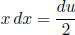. We sub this in to get:

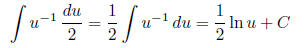
Then we put both parts together to get

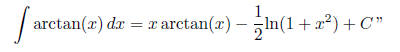
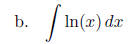
Sample Answer: “This is integrated using IBP [. . .] According to the acronym LIATE ln(x) is
used for u.

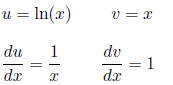
When substituting for

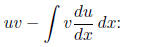
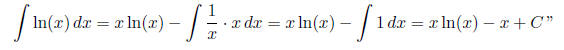
Comment: Most respondents had little trouble with this, and there were many other equally good
solutions given . In part (a), watch out for the re-substitution step at the end: you don’t want to
use your original u = arctan(x) from the IBP instead of u = 1 + x^2 from the u-substitution in the
final answer!

Note, by the way, that you don’t actually need the absolute-value signs in the ln (1 + x^2) term in
part (a), since 1+x^2 will always be positive, and thus equal to its absolute value. And there should
be no absolute- value signs in the x ln(x) term in part (b), because this term isn’t derived from
integrating

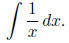
Grading: Ten points for each of the integrals.

3. (25 points) Find each of the following indefinite integrals, stating at each step what method you
need to use and why you need to use it. (For instance: “Now I have to use Integration by Parts
because I have the product of one function times the derivative of another. . . now I can just integrate
directly because this is one of the standard derivatives. . .” and so forth.) A good explanation of
what you think you need to do and why, even if you can’t figure out how to make the formula
come out right, is worth a good chunk of credit!

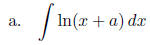where a is any constant. (Hint: Start with a u-substitution and then do IBP.)

Sample Answer: “Start out with u-sub and reincorporate into integral.

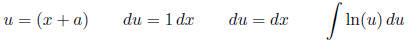
From previous problem we have generalized the answer to the integral ln(x) dx, hence ln(u) du
equals u ln(u) − u + C.

Substitute for u to get answer:

You can also write because a is a constant:

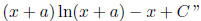
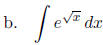
(Hint: Start with the u-substitution )

Sample Answer:
	I start off the problem by doing u-substitution because it is not possible to do Integration by Parts for the first step. In order to make it eas- ier on myself, I designated u a different letter so I did not confuse myself in the long run. u is now p in terms of the equation.
	I designate . Therefore, dp/dx is equal to
	I plug in p and 2p dp to the original equation.
	I set up the Table of the Parts to start Integration by Parts.
	I then plug in the respective pieces into the given equation
	I pull out 2 and take the integral of ep. The integral is the same as the original.
	I then simplify by pulling out ep.
	I resubstitute the value of p = I make sure I add +C. This is the final answer.”

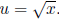Comment: You had to be careful about the order of the steps in part (b); using a different variable
at first (a p-substitution in the sample answer) made it easier to avoid mixing up your u-functions
at the end.

In part (a), you could skip the initial u-substitution if you were comfortable doing IBP directly
on the composed function ln(x + a). But again, if you did do a u-substitution you needed to keep
track of which u is which.

Grading: Ten points for part (a) and fifteen for part (b).

Overall grade: Add up your point scores from each problem. That is your total raw score: use
the table below to convert it to your letter grade for this quiz. (Note that no points are taken off
if your homework is marked “1DL”, that is, “one day late”, since you are allowed to hand in one
assignment one day late with no penalty at any point you choose during the term. If you have been
marked as “1DL” for this assignment, you must hand in all future assignments by the official due
date.)

Note: Half-point scores are rounded up to the nearest whole number ; so if you got a total point
score of, say, 52.5, it counts as an A, not an A-.