Fractions and Rational Numbers
Algebra The Easy Way – Chapter 4
Fractions and Rational Numbers |
Objectives
• Introduction to fractions
• Fraction equivalence, addition, multiplication
• Reciprocals, compound fractions , fraction division
• Rules for fraction use
• Decimal fractions
• Percentages |
Introduction to Fractions
• A fraction consists of two numbers with a divide sign between
– Examples: 1/2, 5/7, 2/3
– Top number: numerator; bottom number: denominator
– Denominator: how many pieces the pie is cut into
– Numerator: now many pieces you get
– If numerator = denominator, result is 1 (whole pie)
• Important: denominator is not allowed to be zero
• Proper fraction: numerator < denominator
• If a, b are any two integers (b != 0), a number written in the
form a/b is called a rational number
• A fraction a/b’s reciprocal is b/a , and a/b x b/a = 1 |
| Math Operations with Fractions
• Multiply or divide top and bottom of a fraction by
the
same number, the value of the fraction stays the same
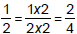
– Resulting fraction is equivalent to the original one
– However, cannot add same number to top and bottom
• Multiplying fractions: just multiply top, bottom numbers
• Adding fractions is easy as long as bottom numbers are
equal—just sum two top numbers, keep bottom number
the same
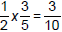
– Using pie slices, I have 2 + 3 = 5 slices of 8
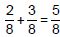
• To add fractions with different denominators, multiply to
get a common denominator, then add
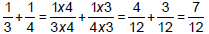 |
• Can multiply a fraction a/b by a rational
number x
• Can also use this same process in reverse to remove (cancel)
portions of a fraction
• Summary of fraction rules (all denominators must not = 0):
Multiplication 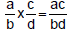
Addition same denominators: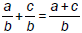
Addition, different denominators: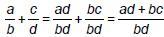
Simplification:
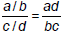
Subtraction:
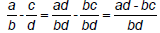
Negative fractions :
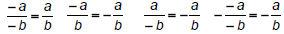 |
Decimal Fractions
• Often difficult to compare fractions with different
denominators
– Can convert to equivalent decimal denominators, then leave
off denominator and add decimal point
– Example: 1/4 = 25/100 = 0.25
• Can convert any decimal fraction in reverse--count fraction
digits (say n), divide by 10^n
– Example: 0.354 = 354/1000
• To multiply, divide fractions: use calculator (rules are given
in the book, but faster to use “machine support”)
• Some rational numbers can’t be represented as decimal
fractions
– Example: 1/3 = 0.333333… |
| Percentages •
Percent: fraction with denominator = 100
– Example: 25/100 = 0.25 = 25 percent
• Percentages often used to indicate change in a quantity
• To calculate a percent change, use
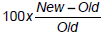
– Note percent decrease is negative if new < old
– Example: old hourly pay = $10, new = $12.50, so
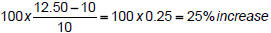
• If g is the percent gain, new value can be found with
new = old(1 + g/100) |
Algebra The Easy Way – Chapter 5
Exponents |
Objectives
• Overview of exponents
• Use of scientific notation
• Rules for exponent use
•Working with negative exponents |
Overview of Exponents
• Exponents are really a shortcut way for writing “multiply a
number by itself some number of times”
– Example: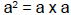 (“a squared”) (“a squared”)
– Example: 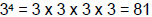
• “Three to the fourth power”
– Example: $1 at 5% for 3 years:
• 1.05 x 1.05 x 1.05 = 1.156725
• General rule for interest in year n:
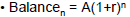
• Where:
– A = initial amount,
– r = interest rate,
– n = number of years |
Scientific Notation
• Another shortcut--for representing very large (or very
small) numbers
– Example: 75 trillion = 75,000,000,000,000
• Same as 7.5 x 10,000,000,000,000
• Then convert the big number to a power of
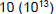
• Final result: 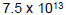
• Can also be written as 7.5E13
– Example: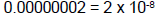 (or 2E-8) (or 2E-8)
• General rule:
– Turn number into one between 1-10
– Count zeros (to the left or right) to get “ten to the”
• Computers often use this method to represent numbers |
Negative Exponents, and More Rules
• If 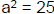 , what is a? , what is a?
– We’ll refer to a as the “ square root ” of 25 (the number, which,
when squared, equals 25)
– Answer: a = 5
– Note -5 x -5 = 25, so there are two possible answers
– When we use the radical symbol ( 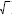 ),
we mean the positive ),
we mean the positive
square root , so 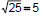
• More useful laws for manipulating exponents:
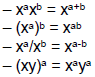 |
Small Fractions to Exponents; Misc. Rules
• Example: 2/100,000
•Write as 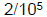
• It then turns out that 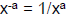 (derivation
on p. 67) (derivation
on p. 67)
• So 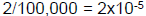
– So negative exponent = 1/positive exponent
– Note 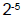 is the reciprocal of (1/over) is the reciprocal of (1/over)
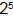
• Other rules/notation:
– Anything “to the zeroth power ” = 1
• So 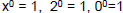 (or =0, or undefined), etc. (or =0, or undefined), etc.
– If x = 0 and n < 0, 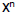 is undefined is undefined
– The symbol “±” means “plus or minus”
• Either the positive or the negative value |
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
January 22nd
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
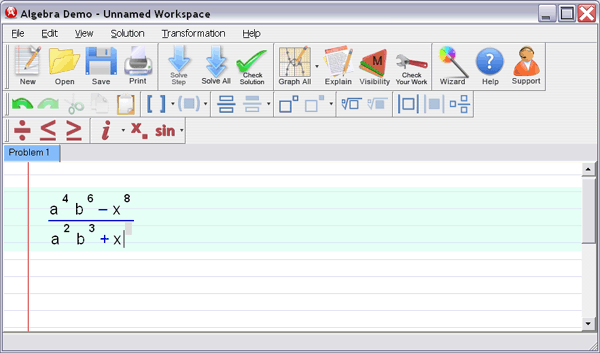
Step 2 :
Let Algebra Helper solve it:
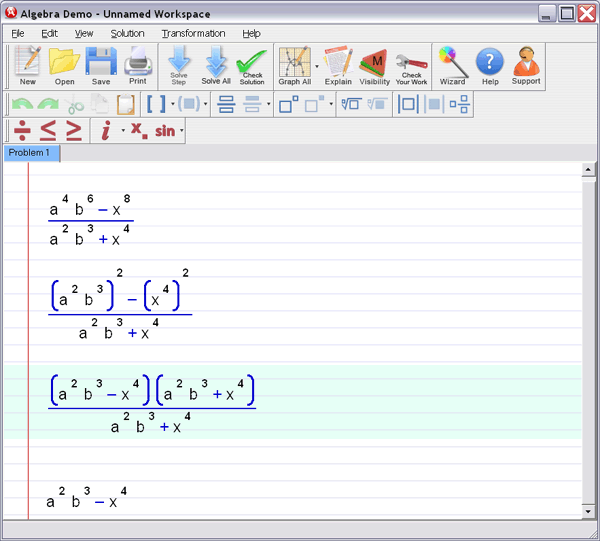
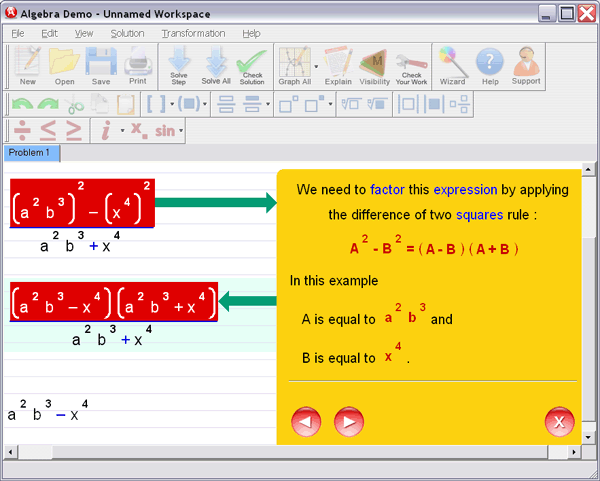
Step 3 : Ask for an explanation for the steps you don't understand:
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



