Objectives: At the end of this lesson, you
should be able to:
1. Define the matrix operations.
2. Apply the matrix operations.
3. Create a matrix equation. |
Matrices create a mathematical structure that has many
properties similar to the real numbers system. They also
have some distinctly different properties . The differences are where the fun
comes in.
Think back on the real number system . We can add, subtract, multiply and applies
powers and apply a
multiplicative inverse to create results the real number system.
We can do the same thing with matrices as long as we obey some simple rules .
Most of the rules require us to
pay attention to the size of the matrix
We can add or subtract matrices of exactly the same size.
We do this by combining the elements within the
matrix in the same (corresponding) position.
Let’s name our matrices A and B where
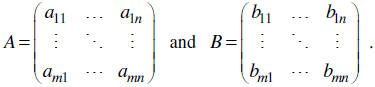
Then 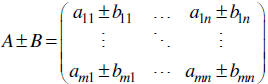
| Notice that this requires the matrices to both
be m×n. If they are not, the sum is not defined . |
Examples:
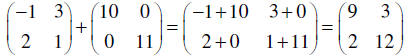 |
The two matrices are both 2×2, so we add element
by
element. |
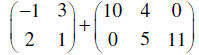 |
These two matrices are different sizes (2×2 and
2×3). We cannot add them.
This is undefined. |
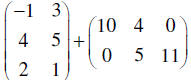 |
These two matrices are different sizes (3×2 and
2×3). We cannot add them.
This is also undefined. |
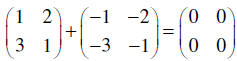 |
The two matrices are interesting! They create a
field of zeroes in the
resulting 2×2 matrix. The two matrices are additive inverses. Every
matrix
A has an additive inverse, called – A. It is created by reversing the
sign of
every entry in A. |
The additive inverses in the example
also creates the zero matrix for the 2×2 set through addition. The zero
matrix has only zeroes in each position. Each size of matrices has its
own zero matrix. It is sometimes
represented by a big, bold zero, 0.
This is also called the additive identity since adding or subtracting it
from any matrix A of the same size,
leaves the matrix unchanged: A ± 0 = A . |
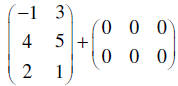 |
Even though it seems like you could write this as
A + 0 , the zero matrix is from a
different-sized set. This is an apples-and-oranges situation and is
still undefined. |
We can multiply matrices when they have a very specific
size relationship. Let’s use about the simplest example
of matrix multiplication to show how it works.
Let A = (a b) . We call this a row matrix since it has only one row.
Let 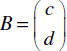 . Recall that this is a column matrix.
. Recall that this is a column matrix.
The multiplication process is a row by column process. We can multiply
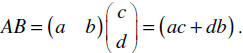
Notice we have a (1×2) times a (2×1) to create a (1×1) matrix. This is called an
inner product (or dot
product). The inner sizes (2 in each case) must match. The resulting size of the
product is the same as the
two outer sizes (1 in each case).
If we try to do BA, we have a (2×1) times (1×2) . It still works, but we create
a (2×2) matrix!
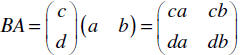
| When we multiply two matrices, the product may
be defined in one direction and not in the other. |
Let 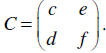 Notice that
Notice that
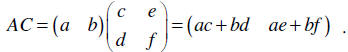 However, CA is not defined
However, CA is not defined
at all.
Similarly,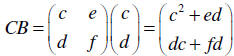 , but BC is not defined.
, but BC is not defined.
You probably wonder why we even care to multiply matrices
in any direction. That’s a fair thought. Let’s create
a couple of examples where we might do such a multiplication.
| Creating a Matrix Equation |
Example: A company has three machines called x1 x2 and x3
which produce the same part. These machines
require 3 hours, 4 hours and 5 hours in maintenance daily.
We can create the row vector of maintenance needs as and the column (3 4 5)
vector of variables
representing the number of each type of machine as
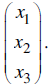
Then the total hours of maintenance is the product
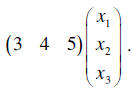
Now this might not seem very much of a savings of writing effort. So let’s add
some more information
about these machines.
These machines can produce 30, 60, and 150 of the same kind of part each in a
day.
That is reflected as the product 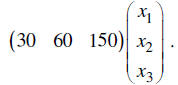
Still seems like a lot of work until we realize we can combine the two
statements in a single product.
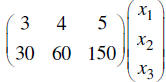
Now when I tell you that the cost of the machines are
$125K; $200K and $350K dollars respectively, you
realize that all of this information can be summarized in the product
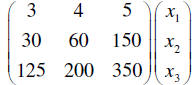
That is definitely using the product to create an
effective summary. If we just stopped there I could be happy
with what I’ve learned. But there is so much more we can do.
Recognize that this is a (3×3)(3×1) to create a (3×1) matrix. What would that
matrix product describe?
Reading back the to first line set -up, you may have caught the word “total.” The
product is the totals of
maintenance hours, production capability and cost of procurement for that same
number of machines.
The finally surprise piece of data is that the company in question schedules 120
daily maintenance hours, needs
a production level of 2400 items, and has a budget of $6.75 million dollars to
buy the machinery.
This creates the (3×1) column matrix of constants
 which reflects these totals.
which reflects these totals.
Now we can complete the package
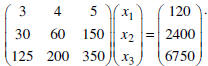
This matrix form is equivalent to the system of equations
to the
right .
I hope I didn’t slip one by you when I scaled the budget line in
thousands. Until I created the final product, I really was playing
I’ve got a secret there.
However, I dropped little pieces of information to show the
thinking as I built the product. The problem would more likely
appear this way:
| System of Equations
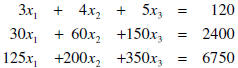 |
Write the matrix equation modeling the following
information:
A company has three machines called x1, x2 and x3 which produce the same
part. These machines require 3
hours, 4 hours and 5 hours in maintenance daily. The company allocates
120 hours to maintenance daily. These
machines can produce 30, 60, and 150 of the same kind of part each in a
day. The company needs to produce
(and sell) 2400 parts daily to meet its contracts. The cost of the
machines are $125K; $200K and $350K dollars
respectively. Finally, the company budgets $6.75 million to buy the
machines. |
Notice the words “matrix equation” in the instructions.
Be careful to respond to the question properly. It is true that both of
the forms boxed to the right reflect the same model when placed in
context. However, each has a proper title. Please use them!
Vocabulary does matter.
Matrix Equation
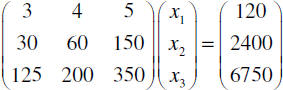 |



