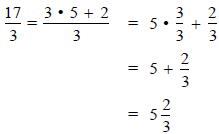When do two fractions represent the same
amount? Or, when do they represent the same
point or number on a number line?
Fold a piece of paper in half:
We now have 2 equal regions:
The shaded part represents
of the paper.
Fold again, the same way.
We now have four equal regions:
the shaded part remains the same,
but now represents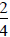 
of
the paper.
Both representations are the same part of the
whole paper.
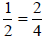
More Equivalent Fractions
Now fold the paper across.
We now have 8 regions of the paper, and the
shaded region now represents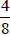 
of the paper.
Notice that can be
written in more than one way.
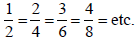
All of these fractions are located at the same
point on the number line. Therefore, they
represent the same number.
Paper Folding to Symbols
From the paper folding exercises we see that
increasing both numerator and denominator of a
fraction by the same factor gives an equivalent or
equal fraction.
It is a crucial step to move toward the use of
mathematical symbols to express these ideas….
More Equivalent Fractions
In symbolic form,
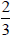can be rewritten as
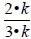for any integer k.
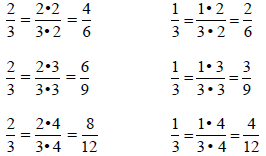
Leading to:
The numerator and denominator
can be divided, or multiplied,
by the same factor to get an equivalent fraction.
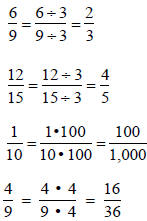
But not all equivalent fractions are related in this
way. For example:
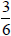and
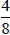each equal
,
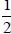But no whole number multiple of 3 gives 4
and
no whole number multiple of 6 gives 8
Similarly
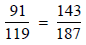
because they both reduce to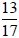 
.
But it is not easy to see that they are equal.
Question
Is there a simple way to tell when any two
fractions are equal?
Yes! It's called "cross multiplication."
Two fractions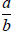 
and
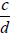are equal if and only if
ad = bc.
For example,
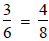because 3 · 8 = 6 · 4
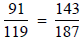because 91 · 187 = 119 · 143
But why does this rule work ?
Explanation for Cross Multiplication
To determine whether
find a common denominator for each fraction.
bd 6 · 8
is a common denominator for both
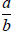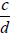
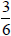and
and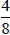
Multiply:
numerator and denominator of
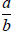by d
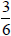by 8
numerator and denominator of
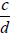by b
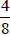by 6
when ad = bc,
(3 · 8) = (4 · 6)
the two fractions are equal.
Cross Multiplication
Perspective: different fractions like
and
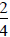
represent the same point on a number line and
therefore , they represent the same number. We
need a simple criterion to decide when two
fractions represent the same number.
Definition 2 Two fractions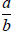and
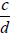are equal,
that is, they represent the same number, if and
only if
ad = bc
Ordering Fractions
The explanation leading to cross multiplication
shows a way to compare unequal fractions.
Proposition: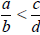
if and only if ad < bc.
Is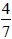 
larger than
?
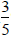Since 4 · 5 < 7 · 3 then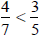 
Is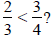
2 · 4 ? 3 · 3
since
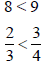
Alternatively,
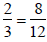and 
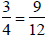
Therefore,
.
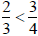Determine Which Fraction is Larger
Worksheet
Which rational number is larger?
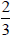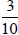or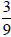
?
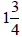or 
?
or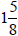 
?
More Equivalent Fractions
Definition 2 includes the cases where some or
all of a, b, c, and d are negative .
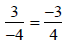
using cross multiplication
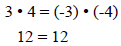
or by multiplying the top and bottom of one
fraction by -1
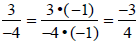
Another example
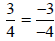
using cross multiplication
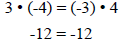
or by multiplying the top and bottom of one
fraction by -1
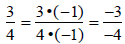
Fractions are Rational Numbers
Definition 3: A rational number is any number
which can be expressed in the form
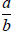where a
and b are integers; b does not equal zero .
Fractions represent rational numbers.
More than one fraction represents the same
rational number,
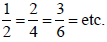
Rational numbers may be thought of as points
on the number line and fractions are the names
we call them.
SETS of NUMBERS
| Rational Numbers any
number that can be expressed in
the form of a/b, b≠0, where a and b are
integers.
Integers
… -3, -2, -1, 0, 1, 2, 3...
Whole Numbers
0
Counting Numbers
1, 2, 3, … |
|
|
|
Addition and Subtraction of Fractions
Case 1
Two fractions which are to be added or
subtracted with the same denominator.
In general
Case 2
Two fractions which are to be added or subtracted
with different denominators.
An important formula for all cases:
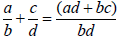
Justification:
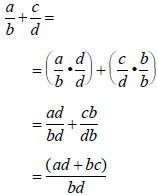
Therefore:
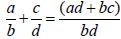
This formula is important in algebra.
Examples
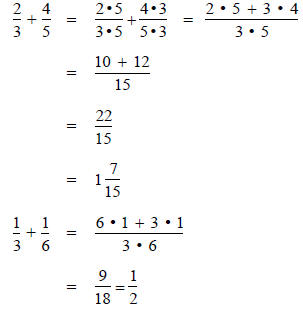
In practice, common denominators less than bd are
used. The lowest common denominator for the
fractions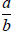and
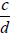is the Least Common
Multiple
( LCM ) of b and d.
More Equivalent Fractions
To justify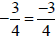 
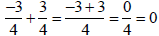
and
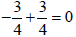
because any number added to its opposite = 0
therefore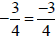
Mixed Numbers to Improper Fractions
An important definition to remember is:
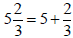
Converting the mixed number to an improper
fraction can be done using addition of fractions.
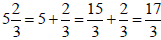
A shortcut to convert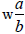 
to
an improper fraction is to
multiply the whole number (w) times the denominator
(b) and then add the numerator (a).
That is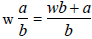 
Example: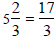 
because 5 · 3 + 2 = 17
Converting a Mixed Number to an Improper Fraction
Worksheet
Explain why these two ways of converting a
mixed number to an improper fraction are really
the same.
By using addition of fractions we get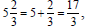 
or by multiplying the whole number times the
denominator and then adding the numerator we get
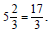
Improper Fractions to Mixed Numbers
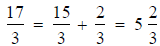
Long division tells us how to do this
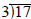gives
5 with remainder 2
or
17 = 3 · 5 + 2
So
