Matrix Operations

Matrix Definitions

A matrix is a rectangular array of numbers called the entries (also called
the elements ) of the matrix. The following are all matrices:

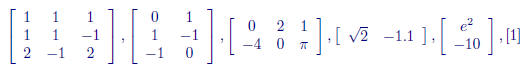
The size of a matrix is the number of rows and columns. An m × n matrix
has m rows and n columns.

Ex: What are the sizes of each of the matrices given above?

Note: A vector is also a matrix. A row vector is a 1 × n matrix (called a row
matrix). Similarly a column vector is a m × 1 matrix (called a column matrix).

The entries of a matrix A are denoted by a_ij where i is the row number and
j is the column number. For example, in

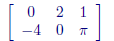
we have a₁₁ = 0, a₂₁ = −4, and a₂₃ = .

Matrix Definitions (2)

We write a general matrix A as

We can also write

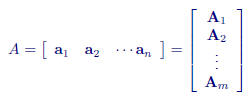
where a_j are the columns of A and A_i are the rows of A.

The diagonal entries of A are a₁₁, a₂₂, . . . . How many diagonal entries are
there if m > n ?

Matrix Definitions (3)

If A is an n × n matrix then it is called a square matrix .

Example of square matrix :

A square matrix with zero nondiagonal entries is called a diagonal matrix

Example of diagonal matrix :

A diagonal matrix with equal diagonal entries is called a scalar matrix .

Example of scalar matrix :

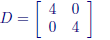
A scalar matrix with values of 1 on the diagonal is an identity matrix .

Example of identity matrix (always called I) :

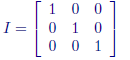
Matrix Operations

Two matrices are equal if they have the same size and the same entries.
The sum of two matrices is defined by elementwise. This makes sense only
if the matrices are the same size.

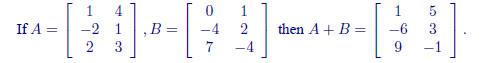
If c is a scalar and A is a matrix then cA is defined by multiplying each entry
of A by c.

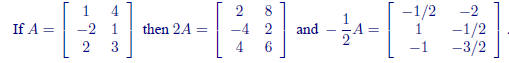
Matrix subtraction is defined as A − B = A + (−B).

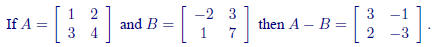
Matrix Multiplication

The product of two matrices is NOT done componentwise. If A is an m × n
matrix and B is an n × r matrix, then the product C = AB is an m × r
matrix given by:

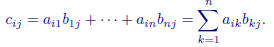
The ij^th entry of C can be thought of as the i^th row of A multiplied by the j^th
column of B.

Note: A and B need not be the same size. The number of rows of A must be
the same as the number of columns of B. In terms of sizes , we have:
m × n · n × r = m × r.

Linear Systems as Ax = b

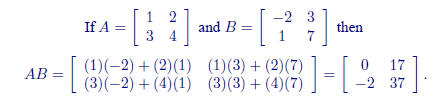
Suppose we wish to solve

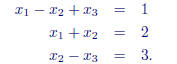
We can write 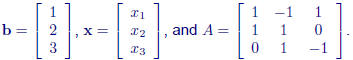Then
solving the linear system is equivalent to solving the system Ax = b for x. In
fact, the augmented system [A|b] really means Ax = b.

Thm: Let A be an m × n matrix, e_i a 1 × m standard unit vector, and e_j an
n × 1 standard unit vector. Then
(a) e_iA is the i^th row of A and
(b) Ae_j is the j^th column of A.
Pf: Do by direct calculation .

Partitioned Matrices

We can write a matrix in terms of submatrices with the matrix partitioned
into blocks . For example, we can write:

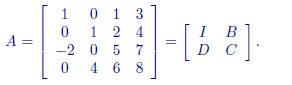
We can partition a matrix into row or column vectors. If B is an n × r matrix
partitioned into column vectors, then 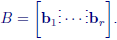If A is m × n then

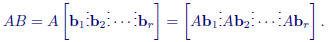
If we write A as row vectors, then using the same idea we can write

Matrix Powers and Transpose

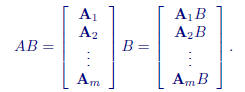
If A is an n × n matrix, then we can define A² = AA, A³ = AAA, etc. As
usual, we define A¹ = A and A⁰ = I.

Thm: If A is a square matrix, and r, s are nonnegative integers, then

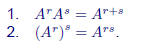
The transpose of an m × n matrix A is the n × m matrix A^T obtained by
interchanging the rows and columns of A. A square matrix A is symmetric
if A^T = A.

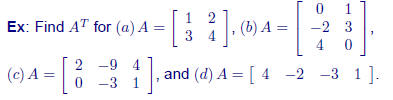
Matlab Matrix Operations

Most usual operations work as expected in Matlab. It will return an error if
you do something incorrectly, like add two matrices of different sizes . The
transpose operator is ′. An identity matrix is formed using the eye command.
A zero matrix can be formed using zeros. Try the following:
» A = [2,3;4,5]
» B = [-2,-1;0,3]
» C = eye(2,2)
» D = zeros(2,2)
» A+2*B
» B-C
» A

Block matrix operations work exactly as expected as well. To define a 4 × 4
block matrix

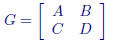
we simply define a 2 × 2 matrix with matrices as elements:
» G = [A,B; C,D]

Matlab Matrix Multiplication

Matrix multiplication brings up an interesting issue in Matlab. Let us say we
wish to find A^k as k → ∞ for

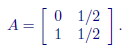
Everything works as expected in Matlab:
» A = [0,1/2;1,1/2];
» A^2
» A^8
» A^16
What does it look like this is approaching ? We find

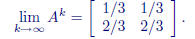
Similarly, we can multiply two different matrices:
» B = [0 1; 1 1; 1 2];
» B*A
» A*B
What will happen when we try A*B? We’ll get an error since A*B is not well
defined?

Matlab Matrix Multiplication (2)

Matlab also has the ability to apply operations to entry individually. If we use
the . command before an operator, then each operation is defined
componentwise. Note that this is ONLY defined for matrices of the same
size.

Using componentwise arithmetic, we have

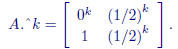
So we can try:
» A.^2, A.^8, A.^16
We find

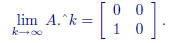
Similarly, we can multiply A componentwise to a matrix B of the same size:
» B = [0 1; 1 1];
» A.*B
» B.*A
Note A. * B = B. * A but in general AB ≠ BA for A and B of the same size.