This Chapter discusses more specialized properties of matrices , such as
determinants, eigenvalues and
rank. These apply only to square matrices unless extension to rectangular
matrices is explicitly stated.
§C.1 DETERMINANTS
The determinant of a square matrix A =
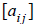is a number denoted by |A| or det(A), through which
important properties such as singularity can be briefly characterized. This
number is defined as the
following function of the matrix elements:
where the column indices
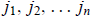are taken from the set 1, 2, . . . , n with no repetitions allowed.
The plus (minus) sign is taken if the permutation (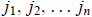
)
is even (odd).
EXAMPLE C.1
For a 2 × 2 matrix,
EXAMPLE C.2
For a 3 × 3 matrix,
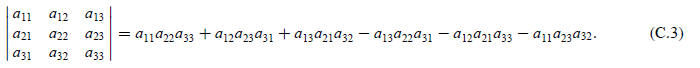
REMARK C.1
The concept of determinant is not applicable to rectangular matrices or to
vectors. Thus the notation |x| for a
vector x can be reserved for its magnitude (as in Appendix A) without risk of
confusion.
REMARK C.2
Inasmuch as the product (C.1) contains n! terms, the calculation of |A| from
the definition is impractical for general
matrices whose order exceeds 3 or 4. For example, if n = 10, the product (C.1)
contains 10! = 3, 628, 800 terms
each involving 9 multiplications, so over 30 million floating-point operations
would be required to evaluate |A|
according to that definition. A more practical method based on matrix
decomposition is described in Remark C.3.
§C.1.1 Some Properties of Determinants
Some useful rules associated with the calculus of determinants are listed
next.
I. Rows and columns can be interchanged without affecting the value of a
determinant. That is
II. If two rows (or columns) are interchanged the sign of the determinant is
changed. For example:
III. If a row (or column) is changed by adding to or subtracting from its
elements the corresponding
elements of any other row (or column) the determinant remains unaltered. For
example:
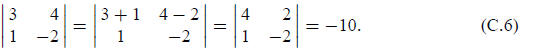
IV. If the elements in any row (or column) have a common factor α then the
determinant equals
the determinant of the corresponding matrix in which α = 1, multiplied by α. For
example:
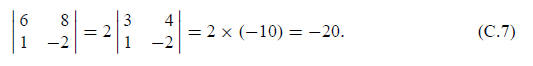
V. When at least one row (or column) of a matrix is a linear combination of
the other rows (or
columns) the determinant is zero. Conversely, if the determinant is zero, then
at least one
row and one column are linearly dependent on the other rows and columns,
respectively. For
example, consider
This determinant is zero because the first column is a linear combination of
the second and
third columns:
column 1 = column 2 + column 3 (C.9)
Similarly there is a linear dependence between the rows which is given by the
relation
VI. The determinant of an upper triangular or lower triangular matrix is the
product of the main
diagonal entries. For example,
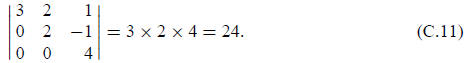
This rule is easily verified from the definition (C.1) because all terms
vanish except
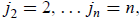which is the product of the main diagonal entries. Diagonal matrices are a
particular case of this rule.
VII. The determinant of the product of two square matrices is the product of
the individual determinants:
|AB| = |A| |B|. (C.12)
This rule can be generalized to any number of factors. One immediate
application is to matrix
powers:
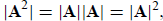and more generally
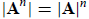for integer n.
VIII. The determinant of the transpose of a matrix is the same as that of the
original matrix:
This rule can be directly verified from the definition of determinant.
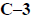
REMARK C.3
Rules VI and VII are the key to the practical evaluation of determinants. Any
square nonsingular matrix A (where
the qualifier “nonsingular” is explained in §C.3) can be decomposed as the
product of two triangular factors
A = LU, (C.14)
where L is unit lower triangular and U is upper triangular. This is called a
LU triangularization, LU factorization
or LU decomposition. It can be carried out in O(n3) floating point operations.
According to rule VII:
|A| = |L| |U|. (C.15)
But according to rule VI, |L| = 1 and
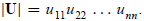The last operation requires only O(n) operations.
Thus the evaluation of |A| is dominated by the effort involved in computing the
factorization (C.14). For n = 10,
that effort is approximately 103 = 1000 floating-point operations,
compared to approximately 3 × 107 from the
naive application of (C.1), as noted in Remark C.1. Thus the LU-based method is
roughly 30, 000 times faster for
that modest matrix order, and the ratio increases exponentially for large n.
§C.1.2 Cramer’s Rule
Cramer’s rule provides a recipe for solving linear algebraic equations in
terms of determinants. Let
the simultaneous equations be as usual denoted as
Ax = y, (C.16)
where A is a given n ×n matrix, y is a given n ×1 vector, and x is the n ×1
vector of unknowns. The
explicit form of (C.16) is Equation (A.1) of Appendix A, with n = m.
The explicit solution for the components
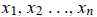of x in terms of determinants is
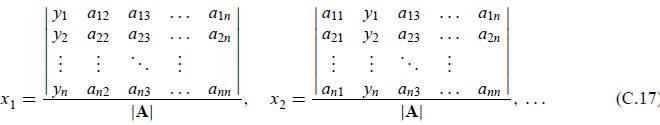
The rule can be remembered as follows: in the numerator of the quotient for xj, replace the jth column
of A by the right-hand side y.
This method of solving simultaneous equations is known as Cramer’s rule.
Because the explicit
computation of determinants is impractical for n > 3 as explained in Remark C.3,
this rule has
practical value only for n = 2 and n = 3 (it is marginal for n = 4). But such
small-order systems
arise often in finite element calculations at the Gauss point level;
consequently implementors should
be aware of this rule for such applications.
EXAMPLE C.3
Solve the 3 × 3 linear system
by Cramer’s rule:
EXAMPLE C.4
Solve the 2 × 2 linear algebraic system
by Cramer’s rule:
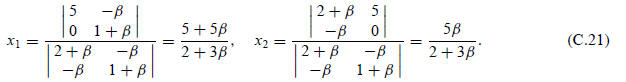
§C.1.3 Homogeneous Systems
One immediate consequence of Cramer’s rule is what happens if
The linear equation systems with a null right hand side
Ax = 0, (C.23)
is called a homogeneous system. From the rule (C.17) we see that if |A| is
nonzero, all solution
components are zero, and consequently the only possible solution is the trivial
one x = 0. The case in
which |A| vanishes is discussed in the next section.
