Relations and Functions

Review:
• Solving Inequalities
• Inequalities with Absolute Value

Properties of Inequalities :

1. Transitive Property
If a < b and b < c , then

2. Addition of Inequalities
If a < b and c < d , then

3. Addition of a Constant c
If a < b, then

4. Multiplying by a Constant c
If a < b and c > 0, then
If a < b and c < 0, then

Note: When multiplying or dividing both sides by a
negative number , reverse the direction of inequality.

Example: Solve the inequality, graph the solution set,
and give the final answers in interval notation.
5 − 6x ≤ 3− x

Example: Solve the double inequality.

−8 ≤1− 3(x − 2) <13

Inequalities Involving Absolute Value

If a is a positive number and u is any expression, is equivalent to −a < u < a is equivalent to u < −a or u > a.

Example: Solve the inequalities.

47

Relation

A relation is a rule of correspondence between two
sets A and B expressed as a set of all ordered pairs
(x, y), where x is an element of A and y is the
corresponding element of B. The domain of a
relation is the set of all first elements in the ordered
pairs, and the range is the set of all second elements
in the ordered pairs.

Example: Relation:{(−1,2),(3,1),(0,2),(−1,−4)}
Domain:
Range:

Function

Note: For a function, no two ordered pairs
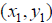
and 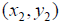have the same first elements, that is,

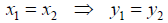
(equivalently, )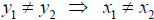

Four Ways to Represent a Function:
1.Verbally (by words)
2.Numerically (by ordered pairs)
3.Graphically (by a set of points in the coordinate
plane)
4. Algebraically (by an equation)

Function Notation: y = f ( x), where x is an
independent variable (argument; input) and y is a
dependent variable ( value of f at x; output).

Testing Relations for Functions:

Example: Determining whether the relation is a
function:
{(1,1),(2,2),(3,3),...}

{(5,5),(2,−3),(5,−5),...}

Example: Determine whether the relation represents
a function.
2x + 3y = 4

x + y² = 4

Evaluating a Function:

Example: If 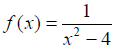, find the following:

f (4) =

f (2) =

f (a + 4) =

Evaluating a Difference Quotient:

Example: For the function f (x) = 3x − 2x² , find and
simplify the difference quotient (h ≠ 0):

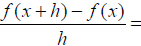
Piecewise-defined Functions:

Example: For the piecewise-defined function

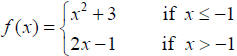
find the following: f (−4) =
f (−1) =
f (2) =

The Domain of the Function:

Example: Find the domain of each function.

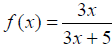
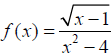
Applications

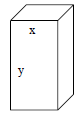
Example: (Volume of a Package)
A rectangular package to be sent by a postal service
has a maximum combined length and girth
(perimeter of a cross section) 108 inches. Assume
that a cross section is a square with a side x. Write
the volume of such a package as a function of x. Find
the domain.

Example: (Cost of Trans-Atlantic Travel)
A Boeing 747 crosses the Atlantic Ocean (3000 mi)
with airspeed of 600 mph. The cost C (in dollars) per
passenger is given by

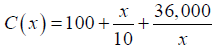
where x is the ground speed (airspeed ± wind speed).
a) What is the cost per passenger for no wind
conditions?

b) What is the cost per passenger with a head wind
of 50 mph?

c) What is the cost per passenger with a tail wind
of 100 mph?

Business Applications:

C = cost
R = revenue
P = profit
x = # of units (demand)
p = price per unit

Formulas:
C = variable cost + fixed costs
R = xp
P = R −C

Example: (Daily Sales)
A doughnut shop sells a dozen doughnuts for $2.95.
Beyond the fixed costs (rent, utilities, and insurance)
of $150 per day, it costs $1.45 for enough materials
(flour, sugar, etc.) and labor to produce a dozen
doughnuts. If the daily profit varies between $50 and
$200, between what levels (in dozens) do the daily
sales vary?

Example: (Geometry)
A rectangle is inscribed in an upper half of a circle of
radius 3 with center at the origin. One side of the
rectangle lies on the x-axis. Two other vertices are
on the graph of the semicircle. Let P = ( x, y) be the
vertex of the rectangle which lies in quadrant I and
on the semicircle. Write the area A of the rectangle as
a function of x and determine the domain of the
function.