1. (4 pts each) Do the following computations with complex
numbers . You don’t need to explain
why you do the computations the way you do, but be sure to show the details of
your work.
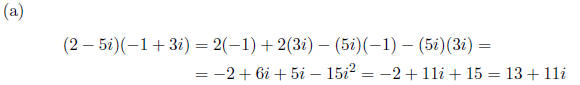
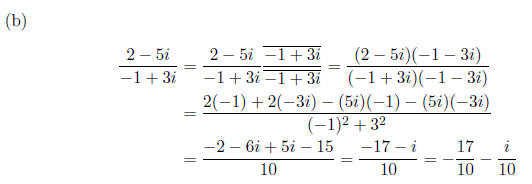
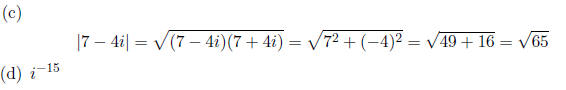
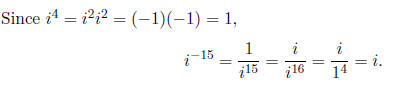
2. (5 pts each) Find the following greatest common
divisors . You don’t need to explain why
you do the computations the way you do, but be sure to show the details of your
work.
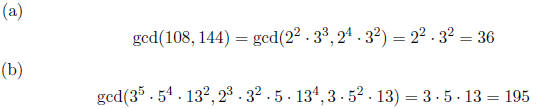
(c) gcd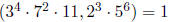
since the two
numbers have no prime factors in common.
3. (5 pts each) Let z = x + yi be any complex number.
(a) Find |z|.
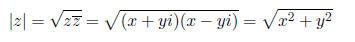
(b) Find 
.
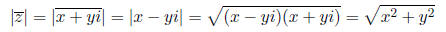
(c) Compare the results of (a) and (b). Explain why this
happens.
They are the same. The absolute value of a
complex number is its distance from 0 in the
complex plane. A number and its conjugate
are mirror images of each other across the real
axis. So their distances from 0 must be the
same.
4. (a) (4 pts) Explain what it means that multiplication
on the integers is associative. Give
an example of this. (You are not asked to prove that multiplication is
associative, only
to explain what the term means .)
It means that (xy)z = x(yz) for any three integers x, y,
z. For example,
(2 · 3) · 4 = 6 · 4 = 24
2 · (3 · 4) = 2 · 12 = 24.
(b) (4 pts) Explain what it means that multiplication on
the rational numbers is associative.
Give an example of this. (You are not asked to prove that multiplication is
associative,
only to explain what the term means.)
It means that (xy)z = x(yz) for any three rational numbers
x, y, z. For example,
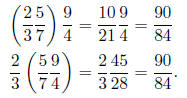
(c) (6 pts) Assume that multiplication is associative on
the integers. Use this to justify that
multiplication is also associative on the rational numbers. (You are now asked
to prove
that multiplication is associative on the rationals.)
Let x, y, z ∈ Q. Then there exist integers m, n, p, q, r,
s such that n, q, s ≠ 0 and x =
m/n, y = p/q, and z = r/s.
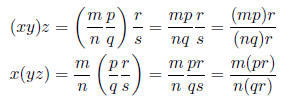
Since multiplication is associative on the integers (mp)r
= m(pr) and (nq)s = n(qs).
Therefore
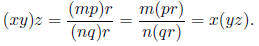
5. Extra credit problem. The quadratic equation x ^2 −3x+5
= 0 has no real solutions. But
it has two complex solutions. You can find them using the usual quadratic
formula .
(a) (4 pts) Find the two solutions of x ^2 − 3x + 5 = 0.
The solutions are
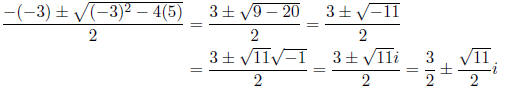
(b) (4 pts) Let A and B denote the two solutions you found
in part (a). Verify (by doing
the actual computation) that (x − A)(x − B) = x^2 − 3x + 5.
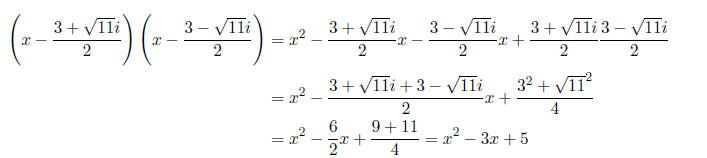
(c) (7 pts) Compute A+B and AB. What do these have to do
with the original equation ?
Explain why this happens.
Actually, notice we already computed A + B and AB in part
(b):
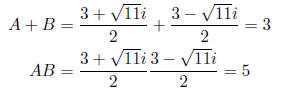
Notice that −(A + B) = −3 is the coefficient of x and AB =
5 is the constant term in
the original equation. This must be so since
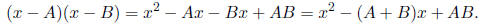
Incidentally, the same is true when the roots are real and
that is standard material in
Algebra I together with the quadratic formula .
