18.03 Class 6, Feb 21, 2006
Roots of Unity , Euler's formula, Sinusoidal functions
[1] Roots of unity
Let a > 0 . Since i^2 = -1 , (+- i sqrt(a))^2 = - a :
Negative real numbers have square roots in C.
Any quadratic polynomial with real coefficients has a root in C ,
by the quadratic formula
x^2 + bx + c = 0 has roots (-b +- sqrt(b^2 - 4c))/2
In fact:
"Fundamental Theorem of Algebra ":
Any polynomial has a root in C (unless it is a constant function).
Special case: z^n = 1 : "n-th roots of unity"
n = 2 : z = +- 1
In general, if z^n = 1 , then |z^n| = 1 , but Magnitudes Multiply ,
so |z| = 1 : roots of unity lie on the unit circle.
n = 3 : Angles Add, so if z^3 = 1 then the argument of z is 0
.....
no, not quite: it could be 2 pi / 3 , since three times that is 2 pi .
It's better to think of the argument of 1 as a choice:
0, or 2 pi, or -2 pi, or 4 pi, or ....
This gives
( -1 + sqrt 3 i ) / 2 .
Or it could be 4 pi / 3 , which gives
( -1 - sqrt 3 i ) / 2
That's it, there's no other way for it to happen. The cube roots of
unity
start with 1 and divide the unit circle evenly into 3 parts.
In general, the nth roots of unity divide the circle into n equal
parts.
How about z^4 = 16 ?
Now the magnitude must be a positive real fourth root of 16, namely, 2:
all the 4th roots of 16 lie on the circle of radius 2. 2 itself is one.
The others have argument such that 4 times the argument is
0, or 2 pi, or ...: so you get +- 2i and +- 2 .
How about z^3 = -8i ?
Well, magnitude must be 2 again. The argument of -8i is 3pi/2, so
one argument of z would be pi/2 : 2i is a cube root of -8i .
The others will differ from that by 2 pi / 3 or 4 pi / 3 . You get a
peace symbol, with verticies at 2i , -sqrt(3) - i , and sqrt(3) - i .
[2] We saw that z' = iz , z(0) = 1 , has solution
z = cos(t) + i sin(t)
We saw this geometrically but you can also just check it:
z' = - sin(t) + i cos(t) = i (cos(t) + i sin(t))
We agreed to write this complex-valued function as e^{it} .
This is "Euler's formula":
e^{it} = cos(t) + i sin(t) .
In fact the same easy check shows that for any complex number a+bi
the solution of z ' = (a+bi) z with z(0) = 1 is
z = e^{at} (cos(bt) + i sin(bt))
so we also agree to define
e^{(a+ib)t} = e^{at} (cos(bt) + i sin(bt)) (*)
That is, the magnitude of e^{(a+bi)t} is e^{at}
and the argument of e^{(a+bi)t} is bt
This definition (*) satisfies the expected exponential rule :
e^{(z+w)t} = e^{wt} e^{zt}
You can see this using the usual rule for real exponentials together
with the angle addition formulas , or by using the uniqueness theorem
for solutions to ODEs. See the Supplementary Notes.
General fact about complex numbers:

Proof by diagram.
______ Apply this to z = e^{it}. I will need to know what
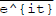 is.
is.
Reflecting across the real axis reverses the angle: so
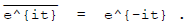
From Euler's formula, (**), and the "general fact" at the start, we find

Sometimes these are also called Euler's Formulas.
Anything you want to know about sines and cosines can be obtained from
properties of the (complex) exponential function.
[3] Sinusoids
A "sinusoidal function" f(t) is one whose graph is shaped like a
(co)sine wave.
I drew a large general sinusoidal function.
I drew the graph of cos(theta) ; this is our model example of a
sinusoid.
A sinusoidal function is entirely determined by just three measurements,
or parameters:
The height of its maxima = depth of its minima = "amplitude," A
The elapsed time till it repeats = the "period" P
or (if spatial) the "wavelength" lambda
Now,
f(t) = A cos( ??? )
For the moment let's suppose t = 0 gives a maximum for f(t)
.
We need to relate t to theta. I drew t and theta axes,
and saw that the relationship is theta = (2pi/P) t .
2pi/P is the number of radians per unit time. It is called the
the "circular" or "angular" frequency of f(t) . It has a special
symbol,
omega. When P units of time have elapsed, so have 2 pi radians.
The "frequency" is simply 1/P .
The offset from the standard picture = "time lag," t_0 .
This is the time at which f(t_0) = A . Usually you make sure 0 =< t_0
< P .
In terms of the parameters A , omega, t_0 , the general
formula for a
sinuosidal function is
f(t) = A cos(omega (t - t_0))
There's another way to express the lag behind the cosine:
= A cos(omega t - phi) where phi = omega t_0
phi is the "phase lag." It's measured in radians. For example
sin(omega t) = cos(omega t - pi/2) .



