• Multiplication
(1) a ∙ b = b ∙ a (commutativity)
(2) 1 ∙ a = a = a ∙ 1 (identity element)
(3) (a ∙ b) ∙ c = a ∙ (b ∙ c) (associativity)
(4) a ∙ 1/a = 1 if a ≠ 0 (inverse element)
Note 1: Rule (4) shows that \division" is an inverse operation of
multipli-
cation.
• Addition
(1) a + b = b + a (commutativity)
(2) 0 + a = a = a + 0 (identity element)
(3) (a + b) + c = a + (b + c) (associativity)
(4) a + (-a) = 0 (inverse element)
Note 2: Rule (4) says that \subtraction" is the inverse operation of addi-
tion.
Note 3: Therefore, if one accepts numbers of the form ( 1/a ) if a ≠ 0,
and
(¡a), one needs to pay attention only to the two operations: multiplication
and addition (instead of four operations: addition, subtraction, multiplica-
tion and division).
• Sign Law :
-(+a) = +(-a) = -a
+(+a) = a = -(-a)
a∙(-b) = -a ∙ b
(-a) ∙ (-b) = a ∙ b
• Distribution Law
a ∙ (b + c) = a ∙ b + a ∙ c
Hence we also have the following:
(b + c) ∙ a = b ∙ a + c ∙ a and
a ∙ (b - c) = a ∙ (b + (-c)) = a ∙ b + a ∙ (-c) = a ∙ b - a ∙ c
• Basic operations involving fractions:
(1) a/b = a ∙ 1/b , if b ≠ 0 (note: a/0 is not defined.)
(2) a/b ∙ c/d = a∙c/b∙d
(3) a/a = 1, if a ≠ 0 (this is law (4) of multiplication.)
(4)
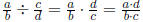(dividing by c/d means multiplication by d/c
.)
For example,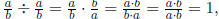 
which shows also that
should be 1.
• Important convention: In an arithmetic expression ,
always simplify paren-
theses and "∙,/"first. Then do \+,-".
For example, (-2 + 3 ∙ 2) - 3 ∙ 5 = (-2 + 6) -15 = 4 - 15 = -11:
• Application
1. Review GCF and LCM (or LCD) from the text.
2. To reduce a fraction a/b to the lowest terms, you can either
(1) divide a and b by their GCF, or
(2) divide a and b by any common factor of a and b, until the resulting
numerator and the denominator have no common factors, or
(3) factorize a and b in terms of prime factors, then cancel the common terms.
For example,
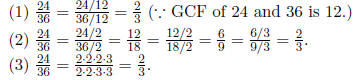
3. To add or subtract fractions , one needs to find their common denomina-
tors first.
For example,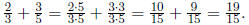 
Note 4: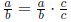 
(since c/c = 1 and multiplication by 1
doesn't change the
number.)
For example,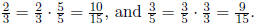 
The idea of solving linear equation of one variable is
pretty simple : We want
to reduce it to the following form first:
a ∙ x = b;
where x is the variable we want to solve, and a and b are known numbers.
(Namely, we collect the terms involving x on the left side of the equality and
the terms not involving x on the right side of the equality.)
Then we divide into the following cases:
(1) If a and b are both zero , namely if you get 0 = 0, then the equation is
always true, no matter what value you assign for x. Therefore in this case,
x can be any number and the equation has infinitely many solutions.
(2) If a = 0 and b ≠ 0, then you get 0 = b ≠ 0, which is absurd. Therefore
in this case, the equation has no solutions.
(3) If a ≠ 0, you can divide on both sides of the equation by a (or what
amounts to the same thing, multiply both sides by 1/a ) to get
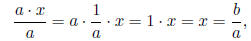
which shows that x = b/a is the solution of the equation.
For example,
(1) Solve 2x + 3 = 0 for x.
solution: Add -3 to both sides of the equality to get 2x+3+(-3) = 0+(-3),
hence get 2x = -3. Then divide both sides of the equality by 2 to get
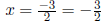: DONE.
(2) Solve (2x - 3 ∙ 2) + 3(x + 5) = 4x - 5 for x.
solution: Simplify the above expression using the basic rules introduced in
the first section, for example apply the distribution law if necessary . For
example, the following procedure would do.
The above equality is equivalent to 2x - 6 + 3x + 15 = 4x - 5, which gives
5x + 9 = 4x - 5. Adding -4x to both sides then gives x + 9 = -5, which
after subtraction by 9 from both sides gives x = -14: DONE.
(3) Solve 3 ∙ (x - 2) = 5 for x.
We can do this in at least two different ways.
1st method: Divide both sides of the equality by 3 to get (x-2) = 5/3 . Then
adding 2 to both sides gives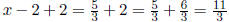 
; and so x = 11/3
.
DONE.
2nd method: Expand the left side by distribution law to get 3x - 6 = 5.
Then add 6 to both sides to get 3x = 11. Then divide both sides as usual
to get x = 11/3 : DONE.
3 Practice Problems
Make sure you can do all of the following problems. Please
let me know if
either you don't know how to do them or if your answers are di®erent from
mine. (See next section for answers.)
1. Factorize the following numbers into prime factors:
(1) 36
(2) 45
(3) 39
(4) 48
(5) 250
2. Find the GCF of the numbers 36, 45, and 48. Find the LCM of them .
3. Simplify the following fractions to the lowest terms:
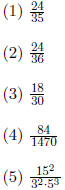
4. Find the least common denominator (LCD) of the
following fractions: 7/6 ,
2/15 and 3/35 ,Then find the sum of these three fractions and write your answer
in lowest terms.
5. Solve 3x -8 = 1 for x.
6. Solve 5x = 18 for x.
7. Solve -2x = 38 for x.
8. Solve 2x + 3 = 4x - 8 - 2x for x.
9. Solve x - 8 + 6x = -4 + 12 - x - 16 + 8x for x.
10. Solve 2(x + 5) - 3 = 8 for x.
11. Solve 3(x - 3) + 6x = -3(x - 2) + 5x - 6 for x.
12. Solve 1/3 (x - 5) + 3x = 3/2 + 1/2x for x.
4 Answers to Practice Problems
1.
(1) 36 = 2 ∙ 2 ∙ 3 ∙ 3.
(2) 45 = 3 ∙ 3 ∙ 5:
(3) 39 = 3 ∙ 13:
(4) 48 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3:
(5) 250 = 2 ∙ 5 ∙ 5 ∙ 5 ∙ 5:
2.
The GCF of 36, 45 and 48 is 3.
The LCM of 36, 45 and 48 is 720.
3.
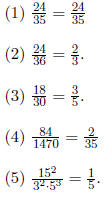
4. The LCD of the three fractions is 210. The sum in
lowest terms is
97/70 .
5. x = 3.
6. x = 18/5 .
7. x = -19.
8. No solutions.
9. x can be any number. (There are infinitely many solutions.)
10. x = 1/2 .
11. x = 9/7 .
12. x = -19/17 .
