In general, mathematical theorems concern the objects in
some set, for example, real numbers
(as in algebra), natural numbers (as in number theory), or points or lines in
some geometry
(whether planar, spherical, on some other surface, or in a higher dimension).
These objects
are assumed throughout to obey some properties, called axioms, which are
essential to proving
results about them. In order to write proper, rigorous proofs, we must know and
state clearly
and explicitly what these properties are . It is also important that the basis
for these axioms
be examined, so that it doesn’t seem as if we are just playing games with rules
made up out of
thin air.
Many of the theorems you will initially be asked to prove
involve real and natural numbers.
There are several reasons for this. These number systems are central to both
science and everyday
life. Real numbers are used to measure continuous quantities such as length,
area, volume,
and mass. Natural numbers are used to count things. You have undoubtedly had
much experience
solving algebra problems involving real numbers, yet you have probably not
proven many
of the results you applied. You also regularly use many basic facts about the
natural numbers,
such as factorization into primes, when doing arithmetic (think about reducing
fractions , for
example) without knowing exactly what you are using or why it is true. In your
future classes,
you will have opportunities to study the theories of geometry, advanced algebra,
and perhaps
advanced number theory, but the basic algebra and arithmetic with which you are
familiar will
be likely be assumed throughout the remainder of your education without
discussion. One day
not too long from now, many of you will teach these basic subjects. This course
may be the
only opportunity you have to thoroughly study the foundation on which they are
built.
The natural numbers are, as we all know, a subset of the
real numbers. On the one hand,
this makes them more limited; certain operations, such as division and
subtraction , are not
defined on them. On the other hand, the fact that the natural numbers are a
smaller (but still
infinite) set with a very special structure makes it possible to prove some
universal assertions
about them that are not true for real numbers in general. For historical
reasons, the theory of
the natural number system is called, simply, number theory. Many theorems in
number theory
are easily stated but surprising, and the existence of intricate patterns in a
number system that
arises simply from counting is a mystery that has fascinated people since the
earliest times.
In developing these number systems, we have two options.
One is to start with the natural
numbers and build, first the rational numbers, and then the real numbers out of
them. The
other is to start with the real number system as a whole and define the natural
numbers as
a specific subset. Humans seem to have a built in natural intuition, much like
our language
ability, about both continuous quantities, such as length and area, and discrete
quantities, such
as numbers of objects, and it is not clear that either approach is better. Both
approaches have
their virtues, and we will in fact discuss both of them. A major virtue of
starting with the real
number system as a whole is that from a logical point of view this approach is
faster, simpler
and easier. So we’ll take it first.
1. Axioms (Initial Assumptions)
The set of real numbers, R, comes with two binary
operations, addition and multiplication.
It is these operations that make R into a number system (as opposed to just a
set). We will not
attempt to define these operations; we will simply assume they exist and obey
certain axioms.
In class we will discuss the meaning of these operations as abstractions of our
experience and
thought process in dealing with continuous quantities, which provides the basis
for the axioms
we will assume about them.
A binary operation associates to each pair of elements of
a set, real numbers in this case, an
element of the same set, often referred to as the result of the operation. In
the case of addition,
this result is called the sum of the pair; in the case of multiplication, it is
called their product.
Every pair of real numbers has a sum and a product. Given two real numbers a and
b, their
sum is denoted by a + b and their product by a · b or, when no confusion will
result, simply
by ab. Because the sum and product are determined uniquely by the numbers
themselves,
the symbols used to represent the numbers do not affect the result: if a = b and
c = d, then
a + b = c + d and ab = cd. It is not necessary to give written justification in
a proof when
making a substitution of this type .
The qualities above constitute the general definition, in
non-technical language, of a binary
operation. Since that term captures these qualities, we won’t list them as
separate axioms.
The properties of addition and multiplication, which we now list, are referred
to as algebraic
properties.
Algebraic Properties of the Real Number System.
There exist binary operations + and
· on R, such that:
(1) These operations are associative:
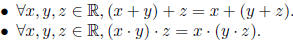
(2) These operations are commutative:
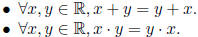
(3) Each operation has a distinct identity element:
• There exists an element
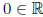such that,
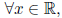x + 0 = x.
• There exists an element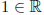 
such that 1 ≠ 0
and, 
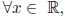x · 1 = x.
(4) All possible inverses exist:
• For each x in R, there exists a y in R such that x + y =
0.
• For each x in R different from 0, there exists a y in R such that x · y = 1.
(5) The operation · distributes over +:
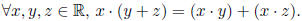
2. Exercises
(1) Prove that 0 is the unique element of R such that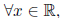
x + y = x. (Suppose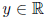 
has the property that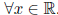 
, x + y = x. Consider y
+ 0 to prove that y = 0.)
(2) Similarly, prove that 1 is the unique element of R
such that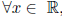 
x · y = x.
(3) Let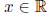 
be a fixed
number. Prove that there is only one element with the property
that x + y = 0. (Suppose x + y = 0 and x + z = 0. Show that y = z.)
We define the additive inverse of x to be this unique
number associated to x and
denote it by −x. We define subtraction by x − y = x + (−y).
(4) Similarly, given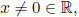 
prove that there is only one element such that xy = 1.
We define the multiplicative inverse of x to be this unique number associated to
x
and denote it by 1/x . We define division by
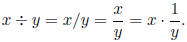
Notice the several notations commonly used for the result
of division. We will generally
use the second or third notation. (The last expression in this chain of
equalities gives the
definition, in terms of the multiplicative inverse and the already postulated
operation
of multiplication.) Note also that, for any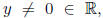 
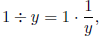
by definition, where 1/y means the multiplicative inverse
of y, and in turn equals
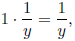
by the multiplicative identity property of 1, so our third
notation for division of 1 by
another number is consistent with the notation we previously chose for the
multiplicative
inverse. (This consistency is important! If the same symbol could represent two
distinct
numbers, our meaning would be unclear from the context in many situations.)
(5) Prove that for any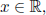 
0 · x = 0. (Hint: use the distributive property.)
(6) Conclude from the preceding result that 0 does not
have an multiplicative inverse. (The
axioms do not assert this. They guarantee that there is a multiplicative inverse
for any
number other than zero , but not the converse proposition that there is not one
for zero.)
(7) Prove that (−1)x = −x. (The left side of the equation
denotes the product of x and
the additive inverse of 1; the right side denotes the additive inverse of x.
These are not
a priori the same number. That they are requires proof.)
(8) Prove that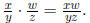 
(Hint:
use the commutative property.)
(9) Prove that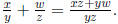 
(Hint:
use the distributive property.)
