PLEASE NOTE THAT YOU CANNOT USE A CALCULATOR ON THE ACCUPLACER -
ELEMENTARY ALGEBRA TEST! YOU MUST BE ABLE TO DO THE FOLLOWING PROBLEMS
WITHOUT A CALCULATOR!
Imaginary Numbers
•Most imaginary numbers result from findings roots of negative numbers given
an EVEN index
only. A purely imaginary number is represented by the letter i and i is equal to
.
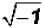Please
note that given an odd index, roots of negative numbers result in rational or
irrational numbers.
NOTE: There is no real number that can be squared to get a result of -1.
Therefore, the solution to
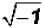only exists in our imagination.
•When we encounter the square root of a negative number,
it is customary to take the negative
sign out of the radical and convert it to the letter i as follows:
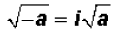
•Furthermore,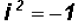 
Complex Numbers
Complex Numbers are of the form a + bi, where a is a real
number and bi a purely
imaginary number with coefficient b . All real numbers can be written in complex
form.
For example, 3 + 0i, -2.34 + 0i, etc.
On the other hand, 3 + 2i or -2.34 - 5.1i are complex
number containing an
imaginary part and are therefore called imaginary numbers.
Problem 1:
Simplify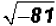 
, if possible,
and write in terms of i.
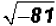is an imaginary number
because the INDEX IS EVEN and the radicand is
negative.
There is no real number that can be squared to get a
result of -81. Therefore, the solution
to 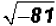only exists in our imagination.
When we encounter the square root of a negative number,
it is customary to take
the negative sign out of the radicand and convert it to the letter "i" as
follows:
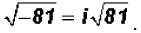There is an assumed
multiplication sign between the number i and
the radical expression.
Since the number 81 is a perfect square, we can further
write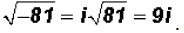 
NOTE: It is customary to write the factor i AFTER a number
once the radical
sign is eliminated .
Problem 2:
Write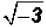 
in terms of i.
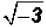is an imaginary number
because the INDEX IS EVEN and the radicand is negative.
There is no real number that can be squared to get a result of -3. Therefore,
the solution
to 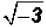only exists in our imagination.
However, we can simplify
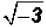by writing
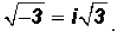
NOTE: It is customary to write the i in front of the
radical!
Sometimes, we want to change the radical expression to a
decimal approximation
(remember it is a non-terminating decimal) in which case we write
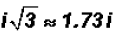
NOTE: It is customary to write the i AFTER a number once
the radical sign is
eliminated.
Problem 3:
Simplify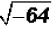 
, if possible,
and write in terms of i.
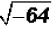is an imaginary number
because the INDEX IS EVEN and the radicand is
negative.
There is no real number that can be squared to get a
result of -64. Therefore, the solution
to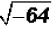 only exists in our imagination.
However, we can simplify by writing
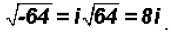
NOTE: It is customary to write the factor i AFTER a number
once the radical
sign is eliminated.
Adding and Subtracting Complex Numbers
•Add or subtract the real parts.
•Add or subtract the coefficients of the imaginary parts.
Problem 4:
Add (3 + 6i) + (9 - 2i).
NOTE: When you carry out an arithmetic operation on complex numbers, you
must enclose them in parentheses !
We can rewrite this as follows:
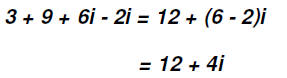
Problem 5:
Subtract (2 + 7i) - (8 - i).
In this case, we MUST observe the minus sign in front of the parentheses.
We first must write 2 + 7i - 8 + i.
The we combine "like" terms to get -6 + 8i .
Please note that i has a coefficient of 1 which is usually
not written, but must
be used in addition and subtraction.
Multiplying Complex Numbers
Multiplying complex numbers uses procedures similar to
multiplying polynomials!
Problem 6:
Multiply 7(3i).
Here we multiply the coefficients to get 21i.
Problem 7:
Multiply 7i(3i).
Here we multiply the coefficients and the imaginary numbers to get
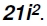
Since we know that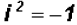
, we can state
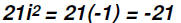
Problem 8:
Multiply (2 + 7i)(8 - 3i).
Use the FOIL process to multiply (2 + 7i)(8 - 3i).
hen
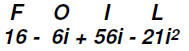
Since we know that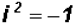 
, we
can write
16 - 6i + 56i - 21(-1) = 16 - 6i + 56i + 21
and finally we can combine like terms to get
37 + 50i
Problem 9:
Factor the Sum of Squares
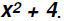
Now we know that the Difference of Squares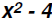 
is
factored into (x - 2)(x + 2).
The Sum of Squares, on the other hand is factored into (x - 2i)(x + 2i).
Check:
Use FOIL to multiply (x - 2i)(x + 2i).
then
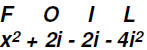
Since we know that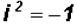 
, we
can write
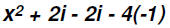
and multiplying and combining like terms will result in
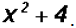
Rationalizing a Denominator containing a Complex Number
•Multiply the denominator by its conjugate ***.
•To preserve the value of the fraction , multiply the numerator by the same
number.
•Simplify all and write the number in the form a + bi.
*** The conjugate of a complex number a + bi is the
complex number a - bi.
NOTE: In Steps 1 and 2 above , we have actually
multiplied the fraction by an
equivalent of the number 1!
Problem 10:
Rationalize the denominator of
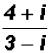and write in standard form a + bi.
First, we will multiply both the numerator and the denominator by 3 + i, which
is the
conjugate of the denominator.
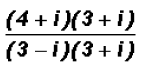
Next, we will use the FOIL method to multiply the complex
numbers in the numerator.
Observe that the denominator contains a Difference of Squares!
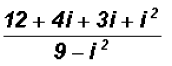
Since we know that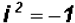 
, we
can write
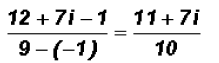
and finally, we find that we can express
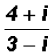in standard form as
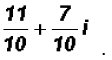
Problem 11:
Rationalize the denominator of
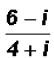and write in standard form a + bi.
First, we will multiply both the numerator and the
denominator by 3 + i, which is the
conjugate of the denominator.
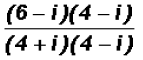
Next, we will use the FOIL method to multiply the complex
numbers in the numerator.
Observe that the denominator contains a Difference of Squares!
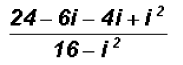
Since we know that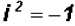 
, we
can write
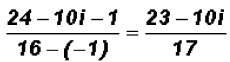
and finally, we find that we can express
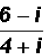in standard form as
.
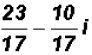Problem 12:
Rationalize the denominator of
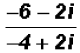and write in standard form a + bi.
First, we will multiply both the numerator and the
denominator by 3 + i, which is the
conjugate of the denominator.
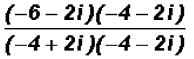
Next, we will use the FOIL method to multiply the complex
numbers in the numerator.
Observe that the denominator contains a Difference of Squares!
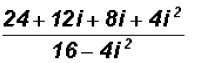
Since we know that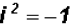 
, we
can write
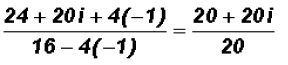
and
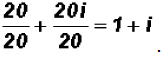
Finally, we find that we can express
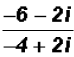in standard form as 1 + i.
