Complex Numbers

Definition

1. ,

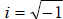i is the building block of complex numbers . It handles the difficulty we usually have to
take a square root of a negative real number . i could be considered the "same" as x in
the expressions . However, i does have the following properties.

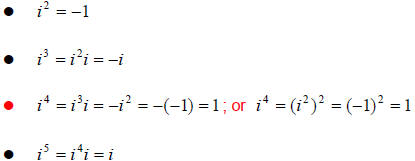
Remark: The powers of I repeat with EVERY 4-th power.

Example 1

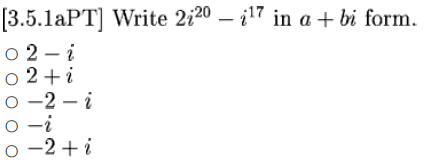
2. Complex number (standard form): a+bi, where a and b are real numbers. a is
called the real part. B is called the imaginary part. Treating i as x, the algebraic
operations for real numbers carry over:
• Equality: a+bi = c+di ⇔ a=c and b=d.
• Addition : (a+bi)+(c+di) ⇔ (a+c)+(b+d)i.
• Subtration: (a+bi)-(c+di) ⇔ (a-c)+(b-d)i.
• Multiplication : (a+bi)(c+di)=ac+adi+bci-bd=(ac-bd)+(ad+bc)i.
The following operations are different from real numbers:
• Conjugate: if z=a+bi, then the conjugate of z is a-bi, denoted by 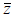. (Conjugate
is to negate the imaginary part.)

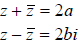
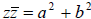,this trick is important in doing complex division . Actually we can
understand this as

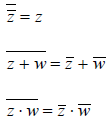
Extra Credit
Show that the above 6 identities are true. Can we interpret the identity
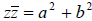
by using the difference of squares formula ?

• Division: if z=a+bi and w=c+di, then

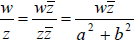
Example 2

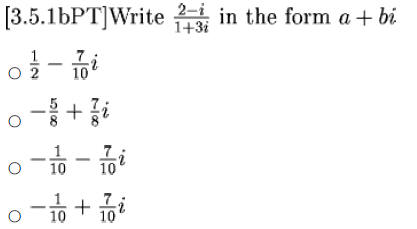
3. Solving Quadratic Equations with NEGATIVE Discriminants
Recall:|

Δ=b² − 4ac >0: TWO x-intercepts

Δ=b² − 4ac =0: ONE x-intercept

Δ= b² − 4ac <0: NO x-intercept (i.e. no real solutions). However, after we have
introduced complex numbers, we know that, by the quadratic formula,
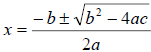, the quadratic function with real coefficients , in this case, will
have a PAIR of CONJUGATE complex numbers as two solutions . (THEY ARE NOT
X- INTERCEPTS THOUGH .)
Remark: How to take square root of a negative number : .

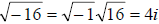Example 3