ORDER OF OPERATIONS
As with any calculator, it is important that the correct
order of operations is used to ensure the correct
answer is found. The appropriate use of parentheses
is critical when typing a problem into the calculator.
Use of parentheses to ensure proper order of
operations
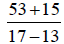
Step 1 Type (53+15) ÷ (17 −13)
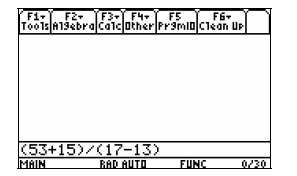
Step 2 Press “ENTER”
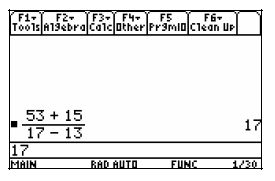
Consider the same problem entered without the
parenthesis.
Notice the answer here is 695/17 because only the 15 is being
divided by the 17. This is not the correct answer to the
problem presented.
The TI-89 will follow the basic rules of operations if
parenthesis are not applied. Consider the problem:
5 + 2× 4 − 2 .
Following the order of operations, the multiplication is
completed first, simplifying the problem to 5 + 8 − 2 .
Then we add and subtract from left to right giving us
the answer 11.
Now do the same problem on the TI-89.
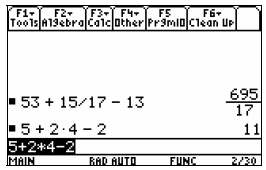
Notice, the answer is given correctly.
Problem Set.
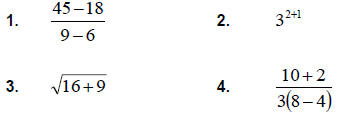
SCIENTIFIC NOTATION
There are many different ways that the TI-89 can
display your answers. The choices vary from scientific
notation to a number with a fixed number of decimal
places or to a number that lets the decimal float. The
TI-89 will show a number with 100 digits or
approximate the same number showing 8 characters
depending on how you set the mode of your calculator.
The following example explores this further using
scientific notation.
Example: Rewrite 5,000,000 in scientific notation:
Step 1: Press the
button
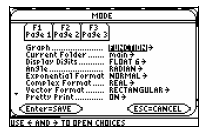
Step 2: Scroll down to Exponential Format. Press
the
button
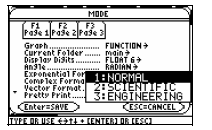
Step 3: Press the
button. Press the ¸ button
Step 4: Press the
button
Step 5: Scroll down to Exact/Approx. Press the
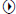button
Step 6: Press the 3 button. Press the
button
Step 7: Enter 5000000 in the entry bar of the
calculator. Press the
button
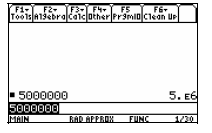
The Answer is 5. E 6 or 5×106
Problem Set
Rewrite each in scientific notation.
1) 7,100,000
2) .12345
3) (432)(367)
4) 23/12345678
FACTORING, GCD, & LCM
Every integer can be rewritten as an unique product of
prime numbers, the process of rewriting numbers as
this product is called factoring.
Factor the integer : 568. To do this enter:
(This accesses the Algebra Menu , and the
factoring command)
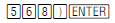
The display should read:
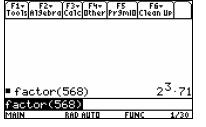
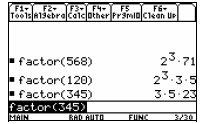
This can be used to find the greatest common divisor
(gcd) of two numbers. For example, to find the gcd of
120 and 345, use the factor operation on each of these
integers, so that the screen will display:
Now take the lower of the two exponents on each
prime occurring. The following table summarizes the
process:
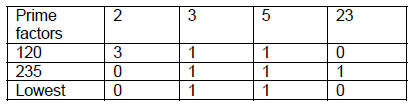
The gcd is thus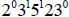 
, or
15. For the least
common multiple (lcm), just take the higher of the two
exponents. Thus the lcm of 120 and 345 is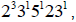 
or 2760.
Problem Set:
1. Factor the integer 12345.
2. Factor the integer 33880.
3. Find the gcd of 12345 and 4200.
4. Find the gcd of 2240 and 65065.
5. Find the lcm of 300 and 120.
6. Find the lcm of 500 and 2783.
The TI-89 is a powerful mathematical tool. The extent
to which the calculator does the calculation is
completely up to the user. It can do steps of the
process or all of the process. This is true for finding
the Greatest Common Divisor (GCD) or the Least
Common Multiple (LCM) of a set of integers.
The calculator can do part of the process, as
demonstrated previously in this lesson, or the
calculator can compute the GCD or LCM directly. Let’s
find the GCD and LCM of 120 and 345.
First turn the calculator on and access the
Menu
by pressing 
. The Screen should look like
this.
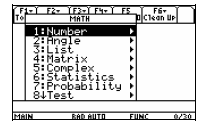
Choose the Number Option and then Scroll down to
the gcd( command.
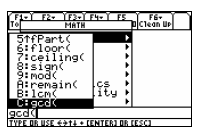
After selecting the gcd( command, type
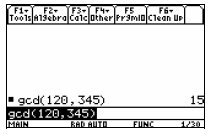
Notice that the calculator output is 15, and this is
consistent with our answer using the factoring method
above.
Let’s repeat this basic process to find the lcm.
First turn the calculator on and access the
Menu
by pressing 
. The Screen should look like
this.
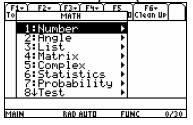
Choose the Number Option and then Scroll down to
the lcm( command.
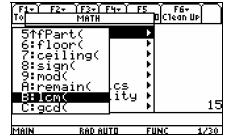
After selecting the lcm( command, type
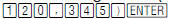
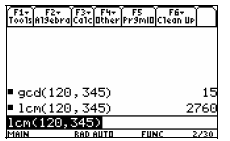
Notice that the calculator output is 2760, and is again
consistent with our answer using the factoring method
above.
Now repeat Problems #3-6 from the pervious problem
set in this lesson using this direct method of finding the
gcd and lcm on your calculator.
Are your answers consistent with what you calculated
above?
EVALUATING EXPRESSIONS
One of the strength of the TI-89 Calculator is that there
are often multiple ways to get solutions to a particular
problem. The following lesson looks at four different
ways to evaluate expressions: first using the “with” key,
second using a table, third using function notation and
fourth using the graph screen .
Evaluating expressions using the WITH Key
If you have a function solved for y, and you want to
know what y equals for a specific x-value, the WITH
key is for you! The WITH key is the 
key just
below
the 
.
For example, suppose y = 4x − 7 . What is y when x
= 3?
Press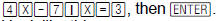 
Your screen
should look like this.
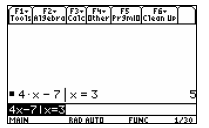
As you can see, the calculator substitutes the value of
3 for x and evaluates the expression. The result, 5, is
displayed at the right.
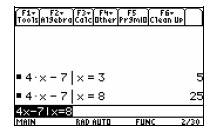
Now suppose we want to know what y equals when x =
8. Instead of typing the expression over again, we can
edit the highlighted expression on the entry line. Press
to remove the highlight, then
to delete the 3.
Press 8 and then 
The with key can be used to evaluate expressions that
have more than one variable . Suppose your want to
find the value of a + 3b when a = 2 and b = 6 .
First evaluate the expression when a = 2 by typing the
following: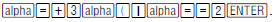
Now evaluate the new expression 3b + 2 when b = 6 ,
by doing the following steps.
Use the up arrow key to highlight the expression
3b + 2 and push enter.
This will copy the
expression to the entry line of your calculator.
Now, using you’re the WITH key, you can type the final
condition of b = 6 . Use the following key strokes:
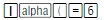
Therefore, our answer is 20.
Problem Set:
1. Use the WITH key to evaluate y=19x+41 for x= 7.
2. Use the WITH key to evaluate y=19x+41 for x=11
