1 Definition of Polynomial
Let D denote the number system we are working over. For our purposes, it will
usually denote Z, Q, or R.
Definition 1. A polynomial in x over D is a finite sum
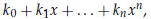
where kj ∈ D for all 0 ≤ j ≤ n and n is a natural number; we use D[x] to denote the
collection of all polynomials in
x over D.
The system D is called the coefficient domain .
The degree of each nonzero term is the exponent of x ; the degree of a nonzero
polynomial is the highest degree of its
terms.
The leading coefficient of a polynomial is the coefficient associated to its
highest degree term.
The degree of a polynomial p(x) is sometimes denoted as deg(p(x)).
Examples of polynomials in x over Q and their degrees are:

When two nonzero polynomials p(x) and q(x) are multiplied,
the degree of the resulting polynomial is the
sum of the original polynomials:
deg(p(x)q(x)) = deg(p(x)) + deg(q(x)). (* )
For this reason, the degree of the zero polynomial is often taken to be either
undefined or -∞: otherwise,
products with the zero polynomial would violate rule (*). For the purposes of
this class, we will define the
degree of the zero polynomial to be -∞, as it will simplify the statements of
some theorems.
2 The Division Algorithm for Polynomials
In class, we performed a few examples of long division with polynomials,
obtaining:
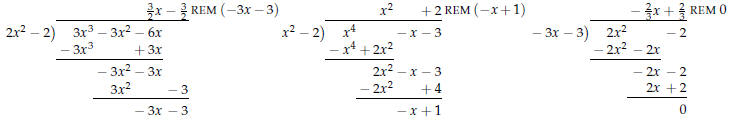
After some discussion about the long division algorithm,
we concluded the following:
Theorem 1 (Theorem 5.16 in the textbook). Let D = Q or R.
Suppose a(x) and b(x) are polynomials in D[x], and assume b(x) ≠ 0. Then there
are unique polynomials
q(x), r(x) ∈ D[x] satisfying the following two conditions:
a(x) = b(x)q(x) + r(x)
deg(r(x)) < deg(b(x)).
Note that if b(x) is a factor of a (x), then r(x) = 0. In this case, deg(r(x)) =
-∞, which is indeed less than
deg(b(x)), as b(x) is nonzero by assumption.
Proof. We must prove existence and uniqueness of the polynomials q(x) and r(x).
As we discussed in class, the long division algorithm yields quotient polynomial
q(x) and a remainder
polynomial r(x) satisfying the conditions of the theorem, giving existence.
The crux of the proof of uniqueness is the following observation:
Lemma. Let 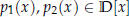 . If
. If
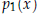 is nonzero and
is nonzero and
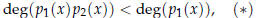
then 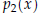 is the zero polynomial.
is the zero polynomial.
Proof of Lemma. We show the contrapositive: if 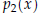 is nonzero, then
is nonzero, then
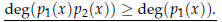
Indeed, if 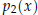 is nonzero then
is nonzero then
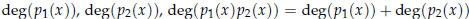 are
are
natural numbers, so 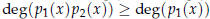 .
.
To show uniqueness, suppose that q(x), q'(x), r(x), r'(x) satisfy
a(x) = b(x)q(x) + r(x), deg(r(x)) < deg(b(x))
a(x) = b(x)q'(x) + r'(x), deg(r'(x)) < deg(b(x)).
It follows that
b(x)(q(x) - q'(x)) = r'(x) - r(x).
Observe that the degree of r'(x) - r(x) at most the largest of deg(r'(x)) and deg(r(x)). (It may not be exactly
deg(r(x)) or deg(r'(x)) because of cancellation.) Both deg(r'(x)) and deg(r(x))
are less than deg(b(x)),
so deg(r'(x) - r(x)) < deg(b(x)). Hence
deg(b(x)(q(x) - q'(x))) = deg(r'(x) - r(x)) < deg(b(x)).
We deduce that q(x) - q'(x) = 0 using our lemma. It follows that r'(x) - r(x)
= 0. We have shown
uniqueness.
Remark. The above theorem does not hold for Z[x]. For example, let a(x) = x2 and
b(x) = 2x.
3 Irreducible Polynomials, Factorizations, and Units
3.1 Irreducible Polynomials
“Prime” is to “integer” as “irreducible” is to “polynomial”.
Definition 2. A nonconstant polynomial p(x) ∈ D[x] is irreducible if it has no
nonconstant factors in D(x) other
than multiples of itself .
If a polynomial is not irreducible, it is reducible .
(Recall that s(x) is a factor of p (x) in D[x] if there is another polynomial
t(x) in D[x] so p(x) = s(x)t(x).)
Example. The polynomials x2 - 2, x, 2x, 4x, x2 + x - 1, and x2 + x + 1 are all
irreducible in Z[x].
The polynomials x2 - 2 and x2 + x - 1 are irreducible in Q[x] and Z[x], but
are reducible in R[x].
The polynomial x2 + x + 1 is irreducible in Z[x], Q[x], and R[x].
3.2 Units
Polynomials, like the integers , are closed under addition, subtraction , and
multiplication; and are not closed
under division. However, there are certain numbers that we can always divide by
and still receive a polynomial;
these numbers depend on the coefficient domain.
Definition 3. An element k ∈ D is a unit if for every polynomial p(x) ∈ D[x],
we have 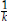 p(x) ∈ D[x].
p(x) ∈ D[x].
The units of Z[x], Q[x], and R[x] are:
| polynomials |
units |
| Z[x] |
±1 |
| Q[x] |
elements of Q |
| R[x] |
elements of R |
Analogously, the units of Z are ±1.



