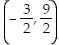Given functions f and g, perform the indicated operations .
Find the domain of the indicated combined function .
30) Find the domain of 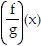 when f(x) =
5x2 - 6x and g(x) = x2 - 2x - 2. |
 |
For the given functions f and g , find the indicated
composition.
Determine which two functions are inverses of each other.
Find the inverse of the one-to-one function.
Does the graph represent a function that has an inverse
function?
Use the graph of f to draw the graph of its inverse
function.
Find the coordinates of the vertex for the parabola
defined by the given quadratic function.
Find the axis of symmetry of the parabola defined by the
given quadratic function .
Find the x- intercepts (if any) for the graph of the
quadratic function .
Find the y- intercept for the graph of the quadratic
function.
Use the vertex and intercepts to sketch the graph of the
quadratic function.
Determine whether the given quadratic function has a
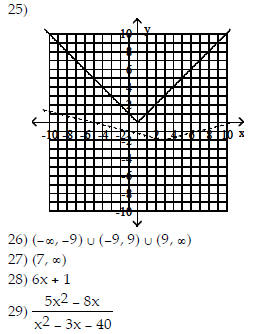
minimum value or maximum value. Then find the coordinates of
the minimum or maximum point.
Answer Key
Testname: MATH1111-STUDY2P
1) -14
2) -2
3) (0, 3)
4) (-1, 1)
5) minimum: (2, -14); maximum: (-2, 18)
6) Even
7) Neither
8) Odd
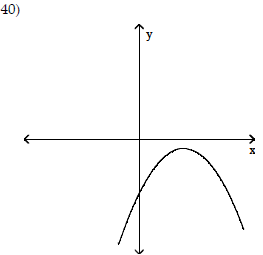
19) intercepts : (0, -2), (-6, 0)
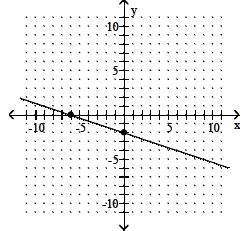
20) y - 2 = -2(x - 3)
21) y = - 3x + 13
22) -34
23) Standard cubic function
24)
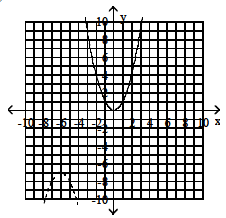
30) Domain: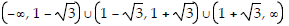 
31)
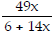
32) x
33) g(x) and h(x)
34) g(x) and h(x)
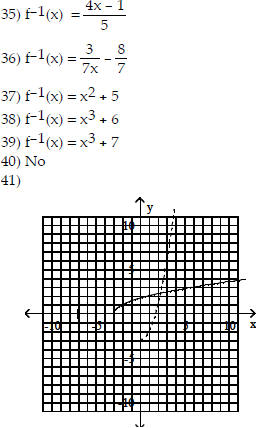
42) (4, -9)
43) (-2, 4)
44) x = -2
45) (0, 0) and (-6, 0)
46) (5, 0) and (3, 0)
47) (0, 0)
48)
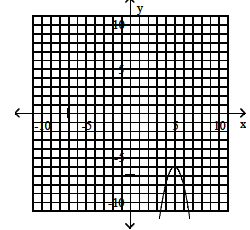
49) minimum;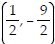
50) maximum;
