Problem A. A rational number is a real number which
can be expressed
as a fraction m/n where both m and n are integers (i.e., 0, ±1, ±2, ±3, . . .)
with n ≠ 0. Assume that x and y are both rational numbers , x^2 + y^2 = 1,
and (x, y) ≠ (0, 1). Prove that there is exactly one rational number r , such
that
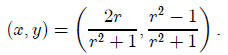
Problem B. In an ordinary game of tennis (not a
“tie breaker” game)
with two players , the first player to win 4 or more points wins the game, if
that
player is ahead by at least two points . Thus, if each player has won 3 points,
play continues until one of the players is two points ahead. Suppose that
Player #1 wins any given point against Player #2 with a fixed probability p
(0 ≤ p ≤ 1). What is the probability f(p) (a function of p) that Player #1
wins a given game against Player #2? Show the derivation of your answer
instead of just stating it. As a test of your answer for f(p), it can simplified
to the form polynomial of degree 7 divided by a polynomial of degree 2.
Rules
The following rules may be changed or
clarified from month to month.
1. Any “regular” undergraduate currently
enrolled at UH Manoa is eligible to compete.
2. Write a complete solution with all details to either problem or both.
3. Submit your solution(s) electronically before the end of the above
month to .For the subject line of your email use “problem of the month” and send
your email via your UH email address . Either write your solution within the
body of your email or within attachment(s) in the form of readable pdf files or
images of your work in jpg format (e.g., scanned or digitally photographed ).
4. Solutions will be judged by a committee of professors according to a
combination of criteria : accuracy, attention to details, chronological order of
submission, and neatness, but not necessarily in that order .
5. Before the end of the 10-th day of the month that follows, the winner(s)
will be announced on the Math Department web site. Moreover, if there
is at least one good answer to a problem the winner(s) for that problem
will collectively receive a total of least $20 to be distributed among them
depending on the criteria in 4 above, as soon as the checks can be extracted
from the Hanf Fund at the UH Foundation, a process that may take several
weeks.