Dense Linear Algebra

Problem:
Some problems can be expressed in terms of linear algebraic operations over dense arrays of data
(i.e. vectors and matrices containing mostly nonzero
values). How does one balance data
movement and computation in order to maximize performance?

Context:

Many problems are expressed in terms of linear operations on vectors and matrices. Common
examples include solving systems of linear equations, matrix factorization, eigenvalue problems,
and matrix multiplication. The way in which a real -world problem is expressed in terms of these
basic linear algebra tasks can be influenced by: (1) the structure of the problem, (2) how a
continuous problem is sampled, (3) how a general solution is expanded in terms of simpler basis
functions.

The pivotal problem in computational linear algebra is how to balance data access costs with the
cost of computation. Given the disparity between memory and CPU speeds, it is critical to
maximize the amount of computation carried out for each item of data accessed from memory.
For problems for which the systems of equations associated with a problem are dense (i.e. they
contain mostly non- zero values ), it is often possible to exploit a “surface to volume” effect
providing plenty of computation to hide the costs of accessing data. Writing software that can
take advantage of this property, however, can be very challenging.

Forces:

Universal forces:

A solution to this problem needs to trade off the cost of recomputing intermediate results as
opposed to storing them and fetching them later.

Overlapping computation with data movement requires software constructed around the details
of a particular memory hierarchy. But this is in direct conflict with the need to write portable
software.

Implementation dependent:

A linear algebra operation may dictate a distinct layout of data to achieve optimal performance.
These data layouts, however, may conflict with those needed by other operations forcing the
programmer to balance data copy overheads with potentially suboptimal
algorithms.

Solution:

General Structure:

Dense linear algebra problems benefit from the fact that they map onto a relatively modest
collection of standard mathematical operations such as the symmetric eigenvalue problem,
multiplication, or LU factorization. Hence, for many operations in linear algebra, a parallel math
library such as LAPACK[2] or ScaLAPACK[3] may provide all that is needed. If this is the case,
the task faced by the programmer is how to define his or her data so the related matrices are in the
format required by the math library.

If a standard library is not available, the programmer can use the Basic Linear Algebra
Subroutines or BLAS. These are available for most architectures on the market and encapsulate
hardware specific assembly code often required to achieve high performance. There are three
levels of BLAS:

· BLAS Level 1: vector/vector operations, O(N) for data movement and computation
· BLAS Level 2: Vector/Matrix operations, O(N²) for data movement and computation.
· BLAS Level 3: Matrix/Matrix operations, O(N²) for data movement, O(N3) for computation.

The BLAS level 3 routines stand out because they have a smaller order exponent for data
movement (O(N²)) than for computation (O(N³)), and, on most parallel systems, can approach the
peak performance available from the system. For this reason, a programmer would benefit from
structuring an algorithm to favor BLAS Level 3 functions. For example, replacing a large number
of dot products (a BLAS level 1 function) with a single matrix-matrix multiplication (a BLAS
level 3 function) can turn a problem bound by memory bandwidth into a compute-bound problem.

If a math library is not available and the BLAS can not be used, or if one needs to implement
BLAS routines from scratch, then it is important to understand how to structure computation in
order to optimize utilization of the memory hierarchy.

We discuss this at a high level in figure 1 for matrix multiplication. The function to multiply two
dense matrices is the basic building block of linear algebra. Various matrix factorizations,
transformations of vector spaces, and many other operations are built from a simple matrix-matrix
multiplication. The Templates series of books, which are freely available electronically, contain
extensive information which guides the reader through the computational organization of various
linear algebra problems [6][7].

There are many ways to organize the computation of a basic matrix-matrix multiplication. Naïve
implementations carry out an inner product for each element of the product matrix. More
sophisticated algorithms construct the function hierarchically from multiplications of smaller
matrix blocks. An algorithm that is close to optimum on most microprocessor based architectures
is based on outer products. An example of this is the SUMMA algorithm described in [1]. The
algorithm must be blocked to make effective use of the memory hierarchy, and if we are to
compute C = C + A* B, a good approach is to work with blocks of A that fit into the L2 cache.
These could be streamed into the registers on the CPU fast enough to overlap with computation if
the related column blocks of C and B could fit in the L1 cache.

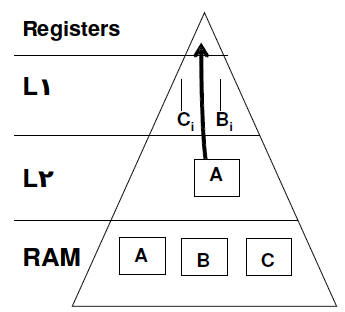	For the BLAS 3 function to compute the matrix product C = C + A * B We use an outer-product with the following blocking: blocks of A which fit in L2 cache so A can be streamed into the registers. Column blocks of C and B to fit in L1 cache TLB large enough to address all the memory in L2
Figure 1: A modern microprocessor with registers, two levels of cache coherent with off chip memory in RAM. Memory latencies decrease as you move up the pyramid but the size (shown by the area of a pyramid segment) drops. Data movement blocked for the BLAS 3 matrix multiply function is shown.

The blocking in dense linear algebra functions is usually not obvious by inspection. The
programmer needs to write their algorithms with flexible blocking built into the loops and then try
a range of blocking factors to find the one that works best. This can be done by hand, but
increasingly this process is being automated [4][5].

As memory hierarchies become more complicated, the programmer working with Linear algebra
must reflect these in their programs. In parallel systems with NUMA architectures or even
distributed memory architectures, distributed arrays are important to consider. These are
discussed at length in the PLPP pattern “Distributed Arrays”. To keep algorithms load balanced,
the array blocks are cyclically distributed so as the algorithm proceeds, all of the units of
execution are kept busy. This technique is heavily used in ScaLAPACK[3].

Invariant:

The discrete representation of the problem (that leads to the matrices and vectors) accurately
represents the original problem and produces well conditioned matrices.

The final result approximates the mathematical definition to within tolerated round-off error.

Example:

Computational Electromagnetics often leads to dense systems of linear equations. For example, in
the late 1980s programs were developed to generate the radar cross section as a function of aircraft
design parameters to reduce the signature of the aircraft (i.e. to support the design of stealth
aircraft).

These simulations of electromagnetic fields use one of two numerical approaches:

1. Method of moments or boundary element method (frequency domain). This method
produces large dense matrices.
2. Finite differences (time domain); which leads to large sparse matrices (which are
sometimes solved by decomposing the sparse system into smaller dense matrices).

These numerical procedures proceed by: i) discretize the surface into triangular facets using
standard modeling tools. ii) represent the amplitude of electromagnetic currents on the surface as
unknown variables . iii) define integral equations over the triangular elements and discretize them
as a set of linear equations. At this point the integral equation is represented as the classic linear
algebra problem:

A x = b

where

· A is the (dense) impedance matrix,
· x is the unknown vector of amplitudes, and
· b is the excitation vector.

Known Uses:

Dense linear algebra is heavily used throughout the computational sciences. In addition to the
electro-magnetics problem we just described, problems from quantum mechanics (eigenvalue
problems), statistics, computational finance and countless other problems are based on dense
matrix computations. Sparse linear algebra is probably more common , but note that many sparse
problems decompose into solutions over smaller dense matrices.

Related Patterns:

This pattern is closely related to a number of lower level patterns depending on the direction taken
in constructing the detailed solution.

Often, the geometric decomposition pattern is used in constructing parallel dense linear algebra
problems.

For matrices represented as hierarchical data structures, the divide and conquer pattern is
indicated.

The data structures used with dense linear algebra problems especially on NUMA or distributed
memory systems are addressed in the Distributed arrays pattern.

And finally, depending on the details of how a problem is represented, a problem can result in
sparse instead of dense matrices (and hence the Sparse Linear Algebra pattern).