Example of Extended Euclidean Algorithm

CRT: Uniqueness

What if x, y are both solutions to the equations ?

• x ≡ y (mod m_i)  => m_i | (x − y), for i = 1, . . . , n

• Claim: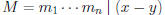

• so x ≡ y (mod M)

Theorem 10: If 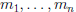are pairwise relatively
prime and m_i | b for i = 1, . . . , n, then 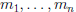| b.

Proof: By induction on n.

• For n = 1 the statement is trivial.

Suppose statement holds for n = N.

• Suppose 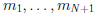relatively prime, m_i | b for
i = 1, . . . ,N + 1.

• by IH, 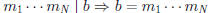c for some c

• By assumption, 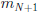| b, so

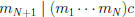
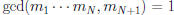• (since m_i’s pairwise relatively
prime => no common factors )

• by Corollary 3,

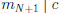
• so

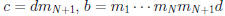
• so .

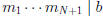An Application of CRT: Computer
Arithmetic with Large Integers

Suppose we want to perform arithmetic operations ( addition ,
multiplication ) with extremely large integers

• too large to be represented easily in a computer
Idea:

• Step 1: Find suitable moduli 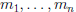so that m_i’s
are relatively prime and 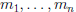is bigger than the
answer.

• Step 2: Perform all the operations mod m_j, j =
1, . . . , n.

o This means we’re working with much smaller numbers
(no bigger than m_j)

o The operations are much faster

o Can do this in parallel

• Suppose the answer mod m_j is a_j:

o Use CRT to find x such that x ≡ a_j (mod m_j)

o The unique x such that 0 < x < 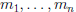is the
answer to the original problem.

Example: The following are pairwise relatively prime:



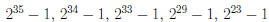
We can add and multiply positive integers up to

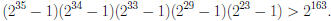
Fermat’s Little Theorem

Theorem 11 (Fermat’s Little Theorem):

(a) If p prime and gcd(p, a) = 1, then 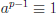(mod p).

(b) For all 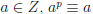(mod p).

Proof. Let

A = {1, 2, . . . , p − 1}

B = {1a mod p, 2a mod p, . . . , (p − 1)a mod p}

Claim: A = B.

• 0 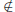B, since 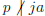, so B 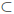A.

• If i ≠ j, then ia mod p ≠ ja mod p

since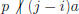

Thus |B| = p − 1, so A = B.

Therefore,

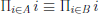  (mod p)


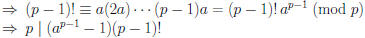
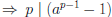[since gcd(p, (p − 1)!) = 1]
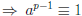(mod p)

It follows that a^p ≡ a (mod p)

• This is true even if gcd(p, a) ≠ 1; i.e., if p | a

Why is this being taught in a CS course?

Private Key Cryptography

Alice (aka A) wants to send an encrypted message to Bob
(aka B).

• A and B might share a private key known only to
them.

• The same key serves for encryption and decryption.

• Example: Caesar’s cipher f(m) = m + 3 mod 26
(shift each letter by three)

o WKH EXWOHU GLG LW

o THE BUTLER DID IT

This particular cryptosystem is very easy to solve

• Idea: look for common letters (E, A, T, S)

One Time Pads

Some private key systems are completely immune to cryptanalysis:

• A and B share the only two copies of a long list of
random integers s_i for i = 1, . . . ,N.

• A sends B the message 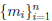encrypted as:

c_i = (m_i + s_i) mod 26

• B decrypts A’s message by computing c_i−s_i mod 26.

The good news: bulletproof cryptography
The bad news: horrible for e-commerce

• How do random users exchange the pad?

Public Key Cryptography

Idea of public key cryptography (Diffie-Hellman)

• Everyone’s encryption scheme is posted publically

o e.g. in a “telephone book”

• If A wants to send an encoded message to B, she looks
up B’s public key (i.e., B’s encryption algorithm) in
the telephone book

• But only B has the decryption key corresponding to
his public key

BIG advantage: A need not know nor trust B.

There seems to be a problem though:

• If we publish the encryption key, won’t everyone be
able to decrypt?

Key observation: decrypting might be too hard, unless
you know the key

• Computing f ^-1 could be much harder than computing
f

Now the problem is to find an appropriate (f, f ^-1) pair
for which this is true

• Number theory to the rescue

RSA: Key Generation

Generating encryption/decryption keys

• Choose two very large ( hundreds of digits ) primes p, q.

o This is done using probabilistic primality testing

o Choose a random large number and check if it is
prime

o By the prime number theorem, there are lots of
primes out there

• Let n = pq.

• Choose e ∈ N relatively prime to (p − 1)(q − 1).
Here’s how:

o Choose 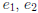prime and about

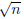
o One must be relatively prime to (p − 1)(q − 1)

* Otherwise 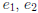| (p − 1)(q − 1)

Find out which one using Euclid’s algorithm

• Compute d, the inverse of e modulo (p − 1)(q − 1).

o Can do this using using Euclidean algorithm

• Publish n and e (that’s your public key)

• Keep the decryption key d to yourself.

RSA: Sending encrypted messages

How does someone send you a message?

• The message is divided into blocks each represented
as a numberM between 0 and n. To encryptM, send

C = M^e mod n.

Need to use fast exponentiation (2 log (n) multiplications)
to do this efficiently

Example: Encrypt “stop” using e = 13 and n = 2537:

• s t o p 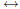18 19 14 15 $ 1819 1415

• 1819¹³ mod 2537 = 2081 and

1415¹³ mod 2537 = 2182 so

• 2081 2182 is the encrypted message.

• We did not need to know p = 43, q = 59 for that.