A. Introduction
1. If we are performing a computation and obtain an answer of
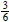 , how are we likely to
, how are we likely to
write that answer? _____
Change the following fractions to simplest form:

2. We are used to the convention of writing a fraction is
in its simplest form. When fractions
contain square roots , they also are generally expected to be written in a
“standard” form.
The standard in this case is that a fraction may not contain any radicals in the
denominator . (The radicals that we will be working with are square roots.) When
radicals
do occur in the denominator (in fractions such as
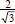 or
or 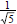 or
or
 ), we must carry out a
), we must carry out a
process known as rationalizing the denominator .
3. Equivalent Fractions
In order to understand the mathematics behind rationalizing the denominator, we
should
look to a familiar example of writing equivalent fractions .
If we were asked to write another fraction which is equivalent to
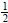 , we might, for
, we might, for
example, write 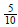 . These
fractions are equivalent since they have the same effect when
. These
fractions are equivalent since they have the same effect when
used in calculations .
We can see below how we mathematically obtain 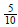 as an equivalent fraction to
as an equivalent fraction to 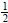 :
:
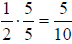
Notice that we multiplied by
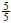 ,and
,and 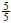 equals 1. We can multiply any
equals 1. We can multiply any
number by 1 without changing the value of the number.
4. Multiplying Square Roots
Before we learn how to rationalize a denominator , we must also remember how to
multiply square roots.
Example: Multiply the following and simplify your answers .

B. Rationalizing the Denominator
1. Consider the fraction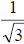 . To rationalize the
denominator, we multiply by
. To rationalize the
denominator, we multiply by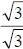 , as
, as
follows:
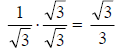
Thus, our final answer is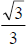 .
.
Some may debate as to whether or not
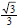 looks any “ simpler ” than
looks any “ simpler ” than
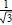 ; nonetheless, this
; nonetheless, this
has become the standard. (Remember that your final answers ARE allowed to have
square roots in the numerator , but your answers may NOT contain square roots in
the
denominator.)
2. Consider the fraction 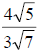 . To rationalize
the denominator, we multiply by
. To rationalize
the denominator, we multiply by 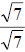 , as
, as
follows:
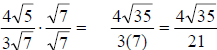
Thus, our final answer is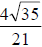 .
.
3. Examples: Rationalize the denominators in the following fractions:

