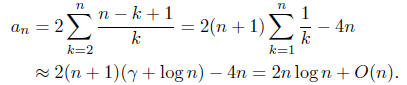1. Some theory.
Formal power series are in one-to-one correspondence with infinite sequences:
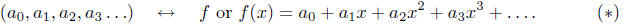
Here the 'x' is just a symbol and f or f (x) is not a function, convergence plays
no role.
But the analogy with functions of a real or complex variable is important and
useful.
Addition and multiplication of formal power series is defined as 'usual' (see
Biggs) and
many conventions used in algebra or calculus are followed. We write, for
example, just 1
for the formal power series
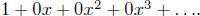
We use f(0) to denote the 'constant term'
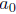of the power series f above. The x
cannot be replaced by any other number, though it can be replaced by a formal
power
series h(x) with no constant term. That is, with f as above, we may consider,
for example,
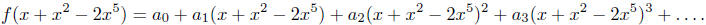
This is allowed because the computation of the coefficient of x n is a finite
procedure, for
any n = 0, 1, 2, ....
The notation f - g = h means f = h + g, and f/g = h means f, g and h are power
series so that f = hg.
Some of the propositions below are in Biggs, others will be discussed in class.
The
statements should not surprise anyone. We will not check everything.
Proposition. A power series f has an inverse 1/f (that is a power series,
of course) if
and only if f(0) ≠ 0.
The formal derivative f' for Df is defined, for f given as above, by
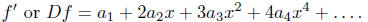
Proposition. For a power series f as in ( *),
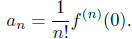
Proposition. For power series f and g,
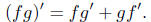
Proposition. For a power series f and an integer m, positive, negative, or zero,
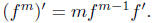
For a nonegative integer k and any z, we define
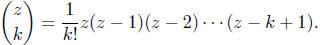
This definition coincides with that of the binomial coefficients when z is also a
nonnegative
integer.
Theorem (the Binomial Theorem for integral exponents ). For
an integer m,
positive, negative, or zero,
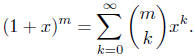
Proof:
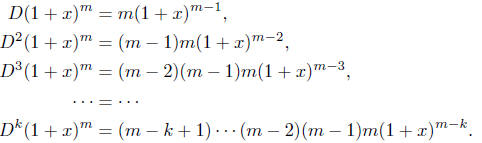
This last expression has constant term m (m - 1)(m- 2) .. (m-
k + 1). The coefficient
of xk in (1 + x)m is thus
.
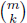Proposition. Let f be a power series with f(0) = 1. Then there is a unique power
series g such that g(0) = 1 and g2 = f. (We write
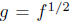.) More generally,
given a
positive integer m, there is a unique power series h so that h(0) = 1 and hm = f
(and
we write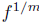 
for this h).
For f a power series with f(0) = 1 and any rational number r, we may then define
fr as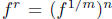 
after we write r = n/m with n and m integers. We should check
that it does not matter whether the fraction n/m is in lowest terms or not.
Proposition. For a power series f and a rational number r, positive, negative,
or zero,
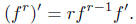
Theorem (the Binomial Theorem for rational exponents). For a rational number
r, positive, negative, or zero,
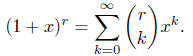
The proof is the same as that of the previous form of the
binomial theorem.
2. Catalan numbers.
The Catalan number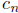 
is the number of ways to bracket or parenthesize a
'product'
of n letters, where the 'product' is a (possibly nonassociative) binary
operation . For
example, there are 5 ways to evaluate abcd, namely
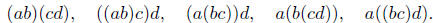
We have
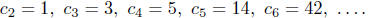
We have seen in class that these numbers satisfy the recursion
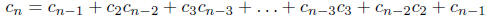
for n = 2, 3, : : :. It will be convenient to let
= 0 and 
= 1 because then
we can write
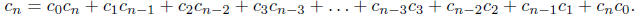
Let
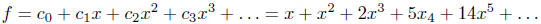
be the generating function of the Catalan numbers. The above recursion means
that the
coefficients of xn in f and f2 are the same for all n ≥ 2. In fact, f
2 - f + x = 0.
By the
quadratic formula (is this OK?),
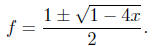
The correct sign is '-' because f has constant term 0.
Then by the binomial theorem,
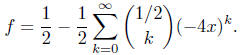
So for n ≥1, comparing the coefficient of xn on both sides of
this equation gives
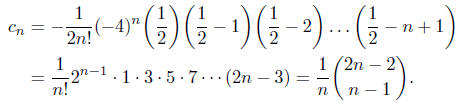
3. Average number of comparisons in QUICKSORT.
Let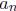 
denote the average number of comparisons the QUICKSORT algorithm re-
quires to sort n distinct numbers. We have
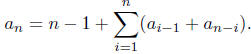
Then
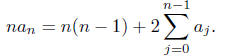
Multiply the above by xn-1 and sum over n = 1, 2, 3,
...
to get
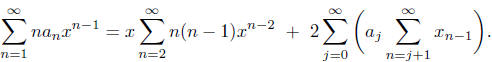
Let f be the generating function for the sequence
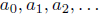(we take 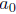to be 0). Then
the above can be written
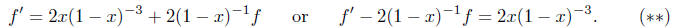
This is a first order linear differential equation.
The method of solving such an equation involves choosing a function (power
series)
u or u(x) so that
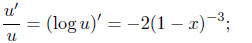
we may take u = (1 - x)2. Multiply both sides of (
**) by u
to get
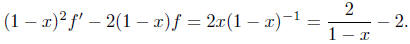
The left hand side is ((1 - x)2f)', so we conclude
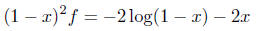
(there is no constant because
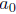= 0), and finally
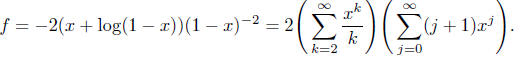
Comparing the coefficient of xn on both sides of the above
equation, we find
