(1) GCF factoring. Factoring out the Greatest
Common Factor is, as we know, simply an application of
the distributive law : ab+ac = a(b+c). We factor out the largest numerical
divisor of all the coefficients (the GCF
of the coefficients) and the least power on any common variable – remembering
that we end up with the same
number of terms inside the parentheses as we had in the original expression. For
example,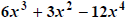 
factors into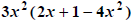 
. GCF factoring is the
most primitive factoring and the easiest. ALWAYS do any
GCF factoring FIRST in any problem where factoring is needed.
(2) Special Products factoring .
(a) Difference of squares . The difference of two squares,
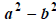, factors into a product of
binomial conjugates : “the first plus the second times, the first minus the
second”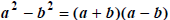 
. For
example,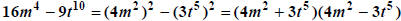 
. The sum of two squares ,
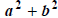, DOES
NOT FACTOR knowing what we know so far. In general, if an expression does not
factor, it is called prime.
(b) Perfect Square Trinomials. Perfect square trinomials are the result
of squaring binomial
sums and differences. Each of the expressions to the right of the “=” below is a
perfect square trinomial.
Hence, if we have a trinomial with the squares of two objects on the “outside”
and either twice their product or the
negation of twice their product “in the middle,” we have a perfect square
trinomial:
For example,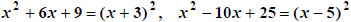 
and more complicated, but
identical in form,
we have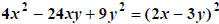 
.
(3) Group and Hope . This is a very specialized method that can be tried
if you have four terms with no
common factor , such as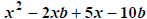 
. The idea is to group
the terms into two sets of two, factor each
group and hope something pops up that is useful. We’ll look at the three
different ways of grouping this
expression and see what happens:
 |
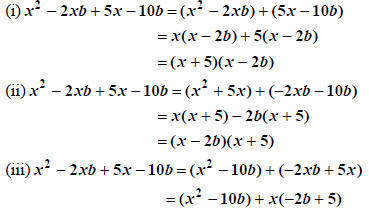grouping terms 1&2 and 3&4 |
|
factor each group and magic! |
|
factor out(x-2b) |
|
grouping terms 1&3 and 2&4 |
|
factor each group and magic again! |
|
factor out (x+5) |
|
grouping terms 1&4 and 2&3 |
|
yuk, no luck here |
If the Group and Hope method works, you will be able to
factor the expression in at least two of the three ways
you can group its terms. So, if one grouping doesn’t work, try another; if that
also doesn’t work, then this method
fails.
(4) Sum and Difference of Cubes.
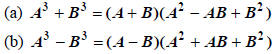
(5) Finally, we come to the fun one – arbitrary
trinomials. Yes, we are talking about things like
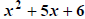which are quadratic trinomials which are not perfect squares. In order to factor
such expressions, we
have to fully understand how they are formed through what you probably call FOIL
but I call LipopR. Examine
carefully the form of the three products below which produce MONIC quadratic
trinomials. (Recall, monic
means leading coefficient is 1.)
For a and b POSITIVE :
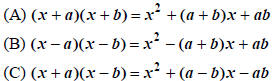
Observe: When the trinomial’s CONSTANT is POSITIVE (cases
(A) and (B)), the two binomials have the same
middle sign. In that case, if the linear coefficient is positive (case (A)), the
binomial middle signs are “ + ”; and if
the linear coefficient is negative (case(B)), the binomial middle signs are “ –
“. The only time the binomial
middle signs are opposite of each other is when the trinomial’s CONSTANT is
NEGATIVE (case (C)). Thus, we
know that if the following trinomials factor, then the factorization has the
stated form.
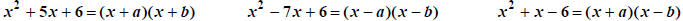
We also observe that the trinomial’s constant (ab)is the
product of the two binomial constants (a and b). So we
just have to think of all the ways the trinomial’s constant factors and check
the resulting ipop (inside product +
outside product) to find the factorization.
Some examples.
 |
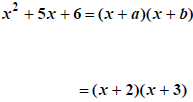ab=6 so we have 1· 6 or 2· 3 |
|
but ipop is 5x so a + b = 5 |
|
try them:1 + 6 ≠ 5, 2 + 3 = 5 |
|
done when found 2 + 3 = 5 |
|
|
|
 |
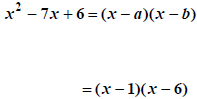ab=6 so again 1· 6 or 2· 3 |
|
ipop is -7x so a +b=7 |
|
try them: 1 + 6 =7, 2 + 3 ≠ 7 |
|
done after 1 +6 =7,but I showed the |
|
other for completeness |
|
|
|
 |
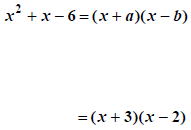ab=6 so again 1· 6 or 2· 3 |
|
ipop is +1x so a - b =+1 |
|
try them:1-6 ≠1, 6-1≠1, 2-3≠1 |
|
3-2=1,finally |
|
|
|
|
|
 |
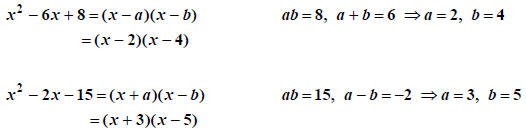