It is the end of fall term. You and your classmates are
very busy and stressed over finals. Your
Math 1 teacher has passed out a “study guide” for the final. This study guide
does not contain
any practice problems, solutions, definitions, page numbers, sections, notes or
anything that seems
helpful. The “study guide” is just a long list of words. Because you and your
friends are so busy,
you each decide to take one of the terms overnight and report back your findings
the next day.
The term you have is LIMITS AT INFINITY. The next day comes but there is no time
to meet.
You must write up everything you’ve learned and slip a copy under each of your
friends’ doors.
Include all relevant definitions, a possible test problem and solution , and a
little bit about why it
is important. Remember how unhelpful the long list of terms was, make your write
up readable
and helpful, like a story .
A limit of a function at infinity looks like this :
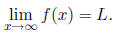
For a function f defined on an interval
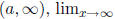f(x) = L means that the values of f (x) can
be made arbitrarily close to L by taking x sufficiently large. Intuitively
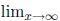f(x) =? is asking,
“What happens to the function f(x) as I plug in larger and larger values of x ?”
If it gets close to
one number, L, then that is the limit of the function at infinity.
Even more accurately, for a function f(x), defined on an
interval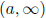 
, we define
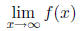
to mean that for every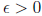 
there is a corresponding number N such that
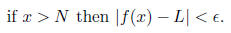
The exact same ideas exist for limits at negative
infinity . so,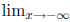 
f(x) means look at the value
of f(x) as we plug in larger and larger negative numbers.
Sometimes this limit does not exist. For example,
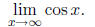
The cosine function oscillates between −1 and 1 even as we
plug in larger and larger numbers. It
never ”settles” on where it wants to be. We say this limit does not exist.
Sometimes a function just keeps growing larger and larger
with larger and larger values of x.
Like f(x) = x^2. We would say,
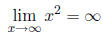
Formally, f(x) = 1
means that for every positive number M there is a corresponding
positive number N such that
if x > N then f(x) > M.
A typical problem may look like this:
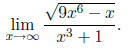
A good method to solve these kinds of problems is dividing
the top and bottom of the fraction by
the highest power of x, and remembering that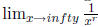 
= 0 if r is a rational number greater
than zero . The solution would look like this:
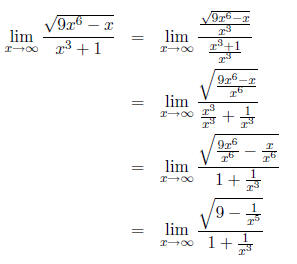
Now, we can think about each piece individually. The
constants don’t change as x goes to infinity,
and both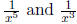 
go to zero. So we get
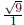which is 3. YAY!
The reason limits at infinity are useful is horizontal
asymptotes. If 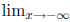f(x) = L, then the
line y = L is a horizontal asymptote for the graph of f (x).
