Combining Like Terms

Like terms :

Like terms are term with exactly the same variables
raised to the exactly the same powers. Any constants in
an expression are considered like terms. Terms that are
not like terms are called unlike terms.

Combining like terms :

Combining like terms is to add or subtract like terms.
Combine like terms containing variables by combining
their coefficients and keeping the same variables with the
same exponents

Example: 3x² – 8x² = -5x²
Example: 5x + 2x = 7x
Example:
3x² + 5x + 2 + x² – x - 3
=3x² + x² + 5x-x + 2-3
= 4x² + 4x - 1

POLYNOMIALS
A Polynomial is a term or sum of terms in which all variables
have whole number exponents .

Example: 2, 3x + 1, ½ x² + 4x + 1,

Not polynomials: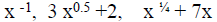

Monomial : Has one term (such as 5x², -6x, 29)
Binomial: Has two unlike terms (such as 2x – 1, x² + 4x)
Trinomial : Has three unlike terms (such as ½ x² + 4x + 1)

The degree of a polynomial is the highest exponent among all
the terms. If the polynomial is a constant, the degree is 0.

The polynomial 3x³ + 5

is a binomial with degree 3.

What type of polynomial is -2x² + x - 3?
What degree is it?

Evaluate this polynomial for x = 3.

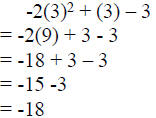
Example 4 p. 414 The polynomial -16t² + 28t + 8
gives the height (in feet) of an object t seconds after it has
been thrown straight upward. Find the height of the object
in 1 second.

The value of the polynomial when t=1 is the height of the
object after 1 second.

Height after 1

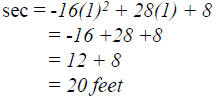
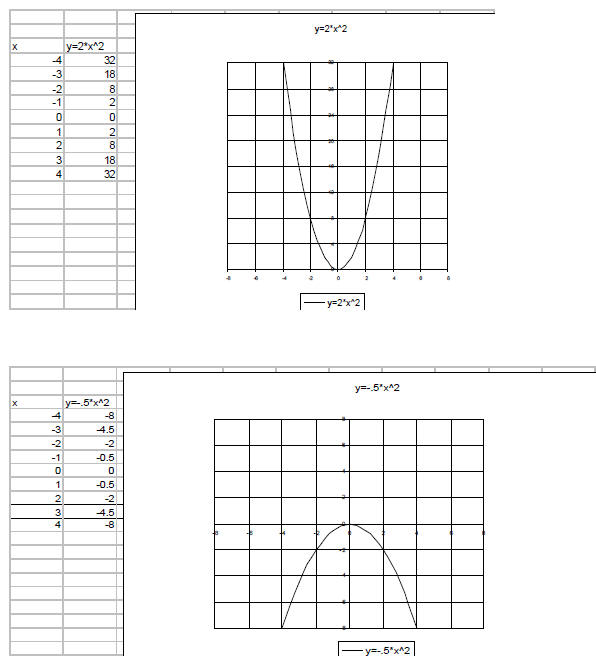
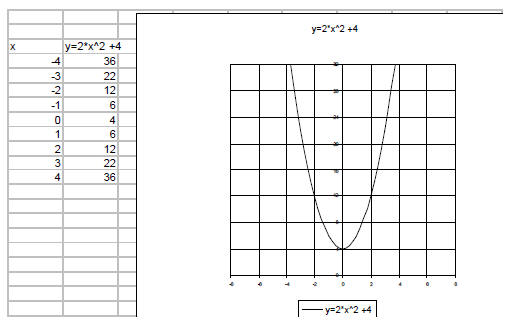
Example 5: Graph y = 2x²

This is not a linear equation because it is degree 2.
This is a parabola.

The coefficient of x² tells us how “fat” or “skinny” the
parabola is. If the coefficient is positive , the parabola is
pointing up. If the coefficient is negative , the parabola is
pointing down.

Since there is no constant added to this equation . The yintercept
is (0,0). When x=0, y=0.

Therefore this parabola is pointing up with it’s y-intercept at
(0,0)