Abstract
We address joint feature selection across a
group of classification or regression tasks. In
many multi-task learning scenarios, different
but related tasks share a large proportion of
relevant features. We propose a novel type
of joint regularization for the parameters of
support vector machines in order to couple
feature selection across tasks. Intuitively, we
extend the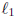 
regularization for single-task
estimation to the multi-task setting. By penalizing
the sum of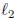 
-norms of the blocks
of coefficients associated with each feature
across different tasks, we encourage multiple
predictors to have similar parameter sparsity
patterns. This approach yields convex, non-
differentiable
optimization problems that can
be solved efficiently using a simple and scalable
extragradient algorithm. We show empirically that our approach outperforms
independent 
-based feature selection on
several
datasets.
1. Introduction
We consider the setting of multi-task learning, where
the goal is to estimate predictive models for several
related tasks. For example, we might need to recognize
speech of different speakers, or handwriting of
different writers, or learn to control a robot for grasping
different objects or driving in different landscapes,
etc. We assume that the tasks are sufficiently different
that learning a specific model for each task results in
improved performance, but similar enough that they
share some common underlying representation that
should make simultaneous learning beneficial. In particular,
we focus on the scenario where the different
tasks share a subset of relevant features to be selected
from a large common space of features.
1.1. Feature selection for a group of tasks
Feature selection has been shown to improve generalization
in situations where many irrelevant features
are present. In particular, penalization by -norm
in the LASSO (Tibshirani, 1996) has been shown to
have interesting properties. Solutions of problems penalized
in -norm are typically sparse in the sense
that only a few of the coefficients or parameters are
non- zero and thus offer models that are more easily
interpretable. Fu and Knight (2000) characterize the
asymptotic behavior of the solutions and their sparsity
patterns and Donoho (2004) shows how for some large
linear systems of equations the regularized solution
achieves in a certain sense optimal sparsity. Recent
papers (Efron et al., 2004; Rosset, 2003; Zhao & Yu,
2004) have established correspondences between the
LASSO solutions and solutions obtained with certain
boosting schemes.
To learn models for several tasks, the regularization
can obviously be used individually for each task.
However, we would like a regularization scheme that
encourages solutions with shared pattern of sparsity. If
we consider the entire block of coefficients associated
with a feature across tasks as a unit, we would like
to encourage sparsity on a block level, where several
blocks of coefficients are set to 0 as a whole.
2. A joint regularization
Formally, let's assume that there are L tasks to learn
and our training set consists of the samples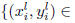 
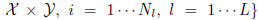where l indexes
tasks and i the i.i.d. samples for each task. Let
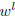be
the parameter vector to be learnt for each task, and
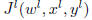be the loss function for each task. Learning
any task independently through empirical risk minimization
with an regularization would yield the optimization problem:
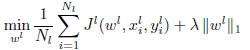
Solving each of these problems independently is equivalent to solving the
global problem obtained by summing the objectives:
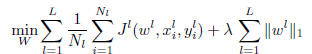
where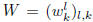 
is the matrix with
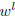in rows or
equivalently with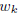 
in columns where
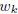is the vector
of coefficients associated with feature k across tasks.
Solving this optimization problem would lead to individual
sparsity patterns for each 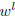. So to select
features globally, we would like to encourage several
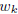to be zero. We thus propose to solve the
problem
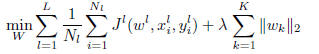
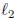i.e., to penalize the -norm of the vector of -norms
of the feature specific coefficient vectors. Note that
this / 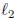regularization scheme reduces to the regularization
in the single task case, and can thus be seen
an extension of it where instead of summing the absolute
values of coefficients associated to features we sum
the euclidian norms of coefficient blocks. The 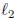-norm
is just used here as a measure of magnitude and one
could also use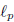 
-norms for
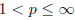and generalize
to /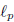-norms.
3. Joint feature selection for multiple SVMs
In this part we specialize to the case where the tasks
are classification tasks, more specifically when the loss
function used is the hinge loss, and we propose an
algorithm to learn the parameter vectors 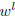for
each
task. W.l.o.g. we assume that for each task we have the
same number n of training examples. The objective
function can then be rewritten as:
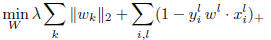
3.1. Reformulation as a constrained
saddle-point problem
The previous objective function is non-differentiable
since neither the hinge loss or the 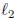-norm are. However
the 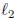-norms can be eliminated by introducing
cone constraints, and the hinge loss through the introduction
of a variable z yielding a bilinear objective
with linear and conic constraints:
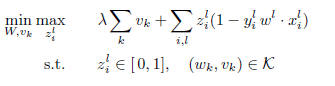
where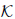 
denotes the usual 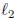cone:
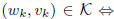
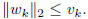Note that the constraint set decomposes
nicely into separate individual constraints on the
variables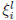 
and pairs of variables
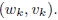
3.2. Extragradient method
The extra-gradient method (Korpelevich, 1976) is a
projection method which is based on the alternation
of two kinds of steps. If we use the notations w =
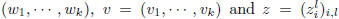with
the superscripts in the following equations indicating
algorithm iterations then we can write the two steps
as:
where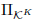 
is the projection on the product of
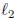-cones
with one cone per feature, and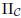 
is the
projection on
the hypercube of dimension nL. Since the objective
is bilinear, the gradient is easily calculated . Besides,
the projections decompose in individual projections for
each variables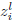 
or
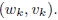We use the specific extragradient
Armijo rule of (He & Liao, 2002). A very similar
derivation gives a saddle point formulation with
conic constraints for -loss regression which can be
solved with the same extragradient algorithm.
4. Applications
4.1. Writer specific OCR
4.1.1. Setting
We apply our method in the context of handwritten
character recognition. Consider, for different writers,
the task of learning to differentiate between pairs of
letters. The simplest approach a priori justifiable if we
dispose of only a few examples of each letter per writer,
but of enough different writers, is to pool all the letters
from all writers and learn global classifiers. We pro-
pose to compare this with our approach which learns
separate classifiers but with similar features, and with
the other naive approach based on individual regularization.
Note that our approach seems intuitively
indicated in this case: every writer draws each letter
somehow by drawing a sequence of strokes. Since we
all learn to write with similar calligraphies, it is likely
that the relevant strokes to recognize an "a" are shared
between different writers.
4.1.2. Data
We use letters from a handwritten words dataset collected
by Rob Kassel at the MIT Spoken Language
Systems Group which contains writings from more
than 180 different writers. However for each writer
the number of examples of each letter is rather small:
between 4 and 30 depending on the letter. The letters
are originally represented as 8 * 16 binary pixel images.
We use a simple stroke model (described in the
next section 4.1.3) to extract a large set of stroke features
from the training set. We then use these strokes
as masks, and construct a representation of each letter
as a long vector of inner product of all the masks with
the letter.
4.1.3. Stroke features construction
We use an ad hoc second order Gaussian Markov
model for the strokes where the speed varies slowly to
privilege straight lines. Following this model we take
a random walk on pixels of the letter, which is furthermore
constrained to move to a neighboring pixel in the
letter at each time step. We run walks of lengths 2, 4
and 6 and call them strokes. To take into account the
thickness of strokes we then add all the pixels of the
letters that are neighbors of the stroke to it. The obtained
stroke is finally smoothed by convolution with
a small kernel. To construct a relevant set of strokes
for the task of discriminating between two letters we
extract strokes in the training set from letters of these
two types and a few from other letter types as well.
The total number of strokes we generated in each of
our experiments is of the order of a thousand.
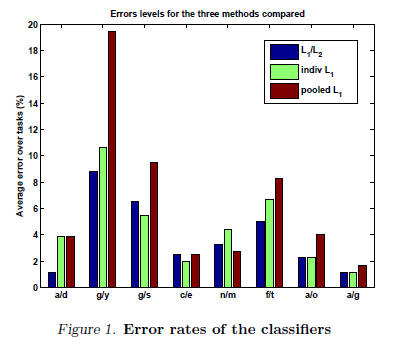
4.1.4. Experiments and Results
We concentrate on the pairs of letters that are the
most difficult to distinguish when written by hand
(see fig.1). We compare three methods: pooling all
the data to build global classifiers with regularized
SVM, learning the classifiers using separate regularization
for each task, and learning the classifier using
our combined / 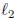regularization.
With such a simple setting, we don't get results which
compete with state of the art methods but error rates
of the order of a few percents. We obtain a 18% improvement
from individual penalization over the results
from pooling, and a further 12% improvement of
/ regularization over individual .
4.2. Multi-class classification
We also applied our algorithm and made a similar com-
parison on a multi-class classification problem. We
used the dermatology UCI dataset, which involves
classifying a disease in six possible diagnostics based
on a list of symptoms. There are 33 different symptoms
which can take 4 different values. We convert
these features in 99 binary features. We work with
training sets of varying sizes from 10 to 200 to illustrate
how the two different regularizations, the regularization
with individual -norms and the / regularization,
perform in different regimes. Our experiments show
that for very small sample sizes as well
as in the asymptotic regime, the two regularizations
perform equally well, but for moderate sample sizes
i.e. around 50 datapoints the / regularization provides
a significant improvement of up to 20% over the
independent regularization.
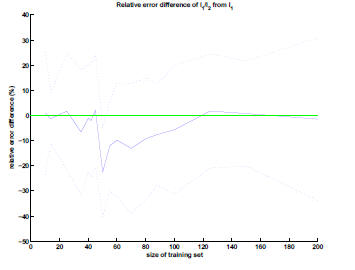
Figure 2. Relative error of / 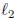regularization with
respect to with error bars at 1SD. Originally and
asymptotically the two regularizations do equally well but
around 50 datapoints / 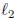does better in relative error.
5. Related Work
There are a few previous approaches to selecting features
for multiple related tasks. In the context of
multi-class classification, Torralba and al. proposed a
joint feature boosting algorithm (Torralba et al., 2004)
to learn all the one-vs-all binary classifiers where the
weak learners of the classical boosting scheme are step
functions applied to individual features. The learners
are selected greedily according to whether they separate
well some bipartition of the set of classes and
among them reduce most the average empirical risk on
all the classifiers of interest. Their work has the advantage
of allowing for non-linear classification, but it
also has a some shortcomings: the choice of the feature
coefficients are tied across tasks, and the restriction
to weak classifiers of bipartitions is can be discussed.
With a broader view, Tony Jebara's work on feature
selection in the context of Maximum Entropy Discrimination
includes a natural extension to the multi-task
setting (Jebara, 2004).
However, none of these approaches relates directly to
the regularization. The /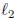-norm appears naturally
in the primal formulation of the Support Kernel
Machine (Bach et al., 2004) where features are selected
by blocks and seems a good candidate to generalize the
-norm.
6. Conclusion
We presented a new regularization scheme for multitask
feature selection, where the different tasks make
a common choice of relevant features. This scheme
provides one possible extension to the multi-task setting
of the usual regularization. We dealt with the
non-differentiability of the / 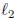regularization by introducing
cone constraints which can be done in general
for any loss, and adapted specifically to the hinge
loss by turning the problem into a saddle-point formulation
solved by the extragradient algorithm. We
showed empirically on two applications that the proposed
regularization which allows for some "transfer"
between the different tasks improves the classification
results in a regime where data is available in relatively
small quantity per task.
