Math 107 Test 2 Solutions

(1) - 10 pts. A wire of length x is bent into the shape of a circle.

(a) Express the circumference of the circle as a function of x.
Solution :
C(x) = x.

(b) Express the area of the circle as a function of x( Recall, A = πr²).
Solution: From (a) we have that C(x) = x = 2πr, so we solve x = 2πr
for r. Thus, r = x/2π . Now plug r into A =πr² to get

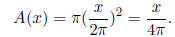
(2) - 10 pts. Determine, without graphing, whether the given quadratic function
has a maximum or minumum. Find the value of the max . or min.

NOTE:You may use your calculator to check but show your work!
Otherwise, I will assume you used your calculator to solve .

g(x) = 4x² - 18x + 7.

Solution: The graph has a minimum because a = 4 > 0, which implies the
graph is pointing up. For any quadratic function, the max/min
occurs at 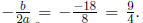So, the min occurs at 9/4 , so the minimum is

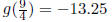
(3) - 10 pts. Suppose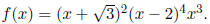

(a) List the real zeros of f and their multiplicity.
Solution:
x = -sqrt(3) has multiplicity 2.
x = 2 has multiplicity 4.
x = 0 has multiplicity 3.

(b) Determine the power function that dictates the behavior of f for
large |x|.
Solution: The power function will have exponent equal to the highest
exponent in the function. If f were expanded out , the highest
exponent would be 2 + 4 + 3 = 9. Thus, p(x) = x⁹ is the
corresponding power function.

(4) - 10 pts. Find the vertical and horizontal asymptotes of

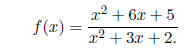
Solution:

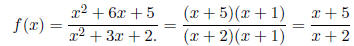
so x = −5 is a vertical asymptote. Now,

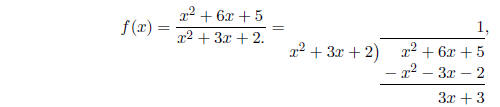
so there is a horizontal asymptote of 1.

(5) - 10 pts. Solve the following inequality algebraically :

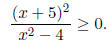
Solution: There is a zero at x = −5. Undefined at x = ±2. So, the intervals
we check are

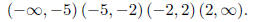
Checking whether positive or negative , and recalling the equation
is 0 at x = −5, yields

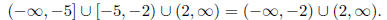
(6) - 10 pts. Let f(x) = 16x⁴ − 19x³ − x² + 2 on [0, 1].

(a) Use the Intermediate Value Theorem to show f has a real zero in
[0, 1].
Solution: f(0) is positive and f(1) is negative , so f has a real zero in
(0, 1).

(b) List all the possible zeros in the interval [0, 1].
Solution: p|2 and q|16, so p = ±1,±2 and q = ±1,±2,±4,±8,±16.
So the possible roots are ±1,±2,±1/2,±1/4,±1/8,±1/16,
but in (0, 1) we only have 1, 1/2, 1/4, 1/8, 1/16.

(7) - 10 pts. Let f be a complex polynomial of degree 6 with zeros: 7+i, −3+i, −i.
Determine the remaining zeros of f.

Solution: Negate the complex part of each root to yield
7 − i, −3 − i, i.

(8) - 30 pts. Dwight K. Schrute and his cousin, Mose, own a beet farm, where they
grow both red and golden beets.

(a) Dwight and Mose have 7000 meters of fencing to enclose a rect-
angular area separating the red and golden beets. On one side of
the rectangular area is the driveway, which will not have fencing
along it(see Figure 1).

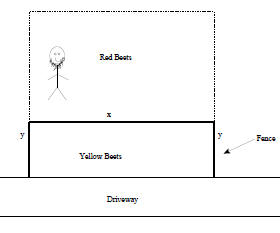
i. Express the area as a function of x.

Solution: The perimeter is given by x+2y = 7000 ! y = 1/2 (7000−
x). Thus the area is

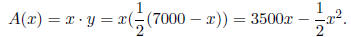
ii. Determine the maximum area that can be enclosed.
Solution: The area function is quadratic so the maximum occurs

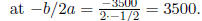So the maximum area is

A(3500) = 6125000.

(b) The price p and quantity x of a pallet of beets is modeled by:

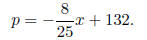
i. Find the revenue as a function of x.
Solution:

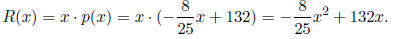
ii. What quantity maximizes revenue?

Solution: Again, this is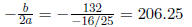

iii. What is the maximum revenue?
Solution: R(206.25) = 13612.5